Objectivo

1. . Construir um gráfico;

2. . Calcular o declive;

3. . Calcular a potência útil a partir da fórmula: Pu = m x c x ∆θ/∆t =› declive

4. . Calcular o valor médio para U e os respectivos desvios de U;

. Dizer qual o valor mais exacto e o mais preciso e porque;

. Calcular a incerteza absoluta de observação;

. Indicar o resultado final;

5. . Calcular o valor médio para I e os respectivos desvios de I;

. Dizer qual o valor mais exacto e o mais preciso e porque;

. Calcular a incerteza absoluta de observação;

. Indicar o resultado final

. Calcular a potência fornecida;

. Calcular o rendimento

Introdução teórica

Porque é que 200ml de água corresponde a 200g?

Concentração mássica

As soluções podem ser mais ou menos concentradas podendo a sua concentração ser obtida utilizando várias formulas, uma delas é a concentração mássica.

P = m/v

P-- concentração mássica (g/dm³); M-- massa (g); V-- volume(dm³)
Unidades S.I (Sistema Internacional)

P = m/v Þ 1 = m/200 ml Û 200 ml x 1 = m Û m = 200g

Declive

∆y/∆x = ∆θ/∆t

Potência útil

Pu = m x c x ∆θ /∆t

Determinação de incertezas quando se fazem várias medições

Quando repetimos várias medições da mesma grandeza em iguais condições, virificamos que se obtêm diferentes valores para essa grandeza, o que revela a ocorrência de erros acidentais.

Um modo de controlar este tipo de erros consiste em efectuar várias medições. O valor mais provável é o valor médio (Xm):

Xm = 1/n(x1 + x2 + x3 + ... + xn)

Verificamos que na maioria dos resultados das medições são diferentes do valor médio. Então, define-se desvio de uma medida di como a diferença entre cada valor xi e Xm:

Di = x1 – Xm

Toma-se como incerteza o módulo do maior dos desvios calculados |dmax|, ou seja, o desvio absoluto máximo. Esta incerteza é designada por incerteza absoluta de observação.

x = Xm ± |dmax|

ou seja, o intervalo para o valor da medida será [Xm - |dmax|, Xm + |dmax|].

Incerteza relativa

É o quociente entre a incerteza absoluta e o valor mais provável:

|dmax| / Xm

Apresenta-se, normalmente, este valor em percentagem.

Exactidão e precisão

Em ciências exprimentais os termos exactidão e precisão têm significados diferentes.

A exactidão indica a proximidade entre os valores medidos e o valor verdadeiro, ou seja, uma medida é exacta se estiver próxima do valor verdadeiro.

Quando existe um valor tabelado, um modo de verificarmos se o valor medido é muito ou pouco exacto é determinado o erro percentual, assim definido:

Erro percentual [%] = (|valor tabelado – valor medido| / valor tabelado) x 100

A precisão traduz a concordância entre os vários valores medidos para a mesma grandeza nas mesmas condições, ou seja, a repetibilidade da medida. Se tivermos várias medidas, há uma grande precisão quando há pouca dispersão dos valores (valores muito próximos entre si) e a mais precisa será aquela cujo desvio é menor, ou seja, a que está mais próxima do valor médio.

Resultado final

x – Xm = |Xmax|

Potência fornecida

Pf = Um x Im

Um = Umedio
Im = Imedio

Rendimento

Para se saber se a potência que se aproveita é muita ou pouca em relação à potência disponivel calculamos o rendimento.

η = Pútil / Pfornecida Þ η = (Pútil / Pfornecida) x 100%

Dados recolhidos

V (água) = 200ml Û m(água) = 200g
Cágua = 4.18 x 10³ J/Kg x º

Resolução dos objectivos propostos

?

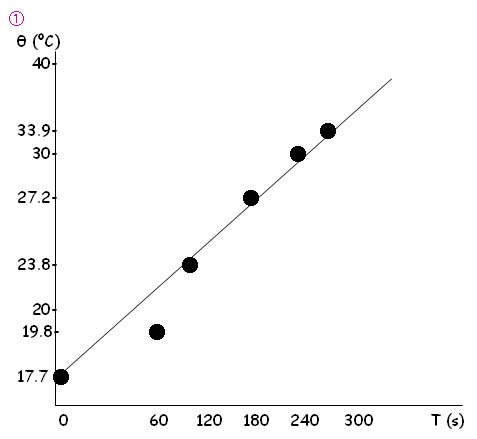
y2 – y1 / x2 – x1  =  30 – 23.8 / 240 – 120  =  6.8 / 120  = 0.05

?

Pu = m x c x ∆θ/∆t

Pu = 0.2 x  4.18 x 10³ x 0.05

Valor médio de U

      (7.22 + 7.25 + 7.26 + 7.27 + 7.26 + 7.27) / 6 = 43.53 / 6 = 7.26

Desvios de U

      di = x1-Xm

      di = 7.22 – 7.26 = - 0.04

      di = 7.25 – 7.26 = - 0.01

      di = 7.26 – 7.26 = 0

      di = 7.27 – 7.26 = 0.01

      di = 7.26 – 7.26 = 0

      di = 7.27 – 7.26 = 0.01

Valor mais exacto e mais preciso porque?

      Erro percentual [%]= |valor tabelado – (valor médio|/valor tabelado) x 100

      (|7.22 – 7.26|/7.22) x 100 = 0.6

      (|7.25 – 7.26|/7.25) x 100 = 0.14

      (|7.26 – 7.26|/7.26) x 100 = 0     mais exacto, pois e o menor. Mais       preciso porque é o que esta mais próximo do valor médio.

      (|7.27 – 7.26|/7.27) x 100 = 0.14

      (|7.26 – 7.26|/7.26) x 100 = 0

      (|7.27 – 7.26|/7.27) x 100 = 0.14

Incerteza absoluta de observação- |dmáx|

      X = Xm ±|dmáx|

      ® 7.22 = 7.26 ±|dmáx|

         ±|dmáx| = - 0.4

         7.26-(-0.4), 7.26+(-0.4)7.22

         7.66, 6.86

      ® 7.25 = 7.26±|dmáx|

         ±|dmáx| = - 0.1

         7.25-(-0.1), 7.25+(-0.1)

         7.35, 7.15

      ® 7.26 = 7.26±|dmáx|

         ±|dmáx| = 0

         7.26-0, 7.26+0

         7.26, 7.26

      ® 7.27 = 7.26±|dmáx|

         ±|dmáx| = 0.1

         7.26-0.1, 7.26+0.1

         7.16, 7.36

      ® 7.26 = 7.26±|dmáx|

         ±|dmáx| = 0

         7.26-0, 7.26+0

         7.26, 7.26

      ® 7.27 = 7.26±|dmáx|

         ±|dmáx| = 0.1

         7.26-0.1, 7.26+0.1 ó 7.16, 7.36

Indicar o resultado final

      x – Xm = |Xmáx|

      7.22 – 7.26 = - 0.04

      7.25 – 7.26 = - 0.01

      7.26 – 7.26 = 0

      7.27 – 7.26 = 0.01

      7.26 – 7.26 = 0

      7.27 – 7.26 = 0.01

? Intensidade

Valor médio de I

      (7.46 + 7.39 + 7.38 + 7.38 + 7.39 + 7.39)/6 Û 44.39/6 Û 7.4

Desvios de I

      di = x1 – Xm

      di = 7.46 – 7.4 = 0.06

      di = 7.39 – 7.4 = -0.01

      di = 7.38 – 7.4 = -0.02

      di = 7.38 – 7.4 = -0.02

      di = 7.39 – 7.4 = -0.01

      di = 7.39 – 7.4 = -0.01

Valor mais exacto e mais preciso. Porque? 

      Erro percentual [%]= |valor tabelado – (valor médio|/valor tabelado) x 100

      (|7.46 – 7.4|/7.46) x 100 = 0.8

      (|7.39 – 7.4|/7.39) x 100 = 0.19¥ mais exacto, pois e o menor. Mais
      preciso porque é o que esta mais próximo do valor médio.

      (|7.38 – 7.4|/7.38) x 100 = 0.3

      (|7.38 – 7.4|/7.38) x 100 = 0.3

      (|7.39 – 7.4|/7.39) x 100 = 0.19

      (|7.39 – 7.4|/7.39) x 100 = 0.19

Incerteza absoluta de observação

      |dmáx|

      x = Xm±|dmáx| 

      ® 7.46 = 7.4±|dmáx|

         ±|dmáx| = 0.06

         7.4 – 0.06, 7.4 + 0.06

         7.34, 7.46

      ® 7.39 = 7.4±|dmáx|

         ±|dmáx| = - 0.01

         7.4 –(-0.01), 7.4 + (-0.01)

         7.41, 7.39

      ® 7.38 = 7.4±|dmáx|

         ±|dmáx| = - 0.02

         7.4 – (-0.01), 7.4 + (-0.02)

         7.42, 7.38

      ® 7.38 = 7.4±|dmáx|

         ±|dmáx| = - 0.02

         7.4 – (-0.01), 7.4 + (-0.02)

         7.42, 7.38

      ® 7.39 = 7.4±|dmáx|

         ±|dmáx| = - 0.01

         7.4 –(-0.01), 7.4 + (-0.01)

         7.41, 7.39

      ® 7.39 = 7.4±|dmáx|

         ±|dmáx| = - 0.01

         7.4 –(-0.01), 7.4 + (-0.01)

         7.41, 7.39

Indicar o resultado final

      x – Xm = |Xmáx|

      7.46 – 7.4 = 0.06

      7.39 – 7.4 = -0.01 

      7.38 – 7.4 = -0.02

      7.38 – 7.4 = -0.02

      7.39 – 7.4 = -0.01

      7.39 – 7.4 = -0.01

?

Calcular a potência fornecida

      Pf = Um x Im

      Pf = 7.26 x 7.4

      Pf = 53.72?Calcular o rendimento

      η = (Pútil / Pfornecida) x 100

      η = ?

      Pútil = 41.8

      Pfornecida = 53.72

      η = (41.8 / 53.72) x 100

      η = 77.81

Conclusão

Desta actividade prático-laboratorial conclui-se que a física implica muitos calculos, e por consequência temos de saber as suas respectivas fórmulas. Assim que falha algum número ou fórmula errada tudo fica mal.

Apreciação global do trabalho

Consideramos que esta actividade foi um pouco difícil devido aos cálculos que tivemos de efectuar, pois houve um certa altura em que me atrapalhei,  mas consegui resolve-lo.

Bibliografia

Informação de texto:

10 F A, Física e Química A – FÍSICA, Bloco 1 – 10/11º ano, Texto Editores

Caderno diário de Física

Outros Trabalhos Relacionados