Trabalhos de Estudantes  

Trabalhos de Física - 12º Ano

 

Ficha do trabalho:

Pendulo Gravítico

Autores: Luís Rita

Escola: Escola Secundária Eça de Queirós

Data de Publicação: 03/01/2014

Resumo: Relatório experimental sobre o pendulo gravítico, realizado no âmbito da disciplina de Física (12º ano). Ver Trab. Completo

Classifique este trabalho:

0 visualizações

Se tens trabalhos com boas classificações, envia-nos pois só assim
o nosso site poderá crescer.

 

Pendulo Gravítico

Objetivos

 

Os objetivos desta atividade experimental e consequente relatório foram:

 

· Identificar as forças que atuam num pêndulo gravítico;

· Identificar as componentes normal e tangencial da força resultante, tal como as expressões das respetivas componentes normal e tangencial da aceleração;

· Identificar o movimento de um pêndulo com oscilações de pequena amplitude como um movimento harmónico simples (MHS);

· Concluir que o período do movimento de um pêndulo depende da amplitude de oscilação mas é praticamente independente desta se ela for reduzida;

· Estabelecer uma relação entre o período do movimento de um pêndulo e o seu comprimento em oscilações de pequena amplitude;

· Concluir que o período de um pêndulo com oscilações de pequena amplitude não depende da sua massa;

· Exprimir o período de um pêndulo com oscilações de pequena amplitude em função da acelaração gravítica e do comprimento do fio;

Determinar experimentalmente a aceleração da gravidade.

Introdução Teórica

Em Mecânica, um pêndulo gravítico é um instrumento ou uma montagem que consiste num objeto que oscila em torno de um ponto fixo. O braço executa movimentos alternados em torno da posição central, chamada posição de equilíbrio. O pêndulo é muito utilizado em estudos de força/peso e de movimentos oscilatórios.

Durante muitos anos o pêndulo foi o “coração” dos relógios. Foi Galileu quem começou por estudar o pêndulo, imaginando-o como um possível relógio. Diz-se que foi ao observar as oscilações de um candelabro na catedral de Pisa que Galileu compreendeu a relação entre a força resultante aplicada a um corpo e as características do seu movimento.

Galileu descobriu, assim, o isocronismo das oscilações do pêndulo ao comparar o número das suas próprias pulsações com o movimento do candelabro.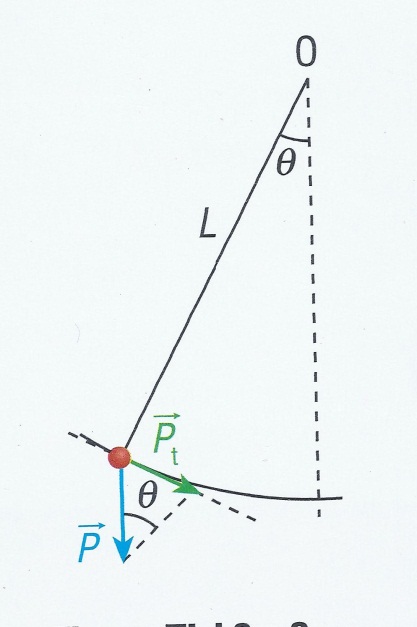

 

Um corpo suspenso por um fio pode constituir um oscilador, pois se for afastado da posição de equilíbrio tende a oscilar naturalmente com um período que lhe é próprio. Um fenómeno é periódico quando se repete ao fim de um certo tempo, T, a que chamamos período. O período e a frequência são usados para caraterizar os movimentos periódicos.

Mas a amplitude (afastamento máximo relativamente à posição de equilíbrio) é também outro parâmetro importante no estudo do movimento pendular.

O período do movimento de um pêndulo depende da amplitude de oscilação, mas, se a amplitude for pequena, (<10°) o período é praticamente independente desta.

Com base na figura 1, podemos escrever:

.

A componente tangencial da força responsável pela alteração do módulo da velocidade do pêndulo é diretamente proporcional a . Deste modo, o movimento não é harmónico simples. O período do movimento depende da amplitude das oscilações.

Já, se as amplitudes de oscilação forem pequenas, de modo que  = , verificar-se-á o isocronismo das mesmas.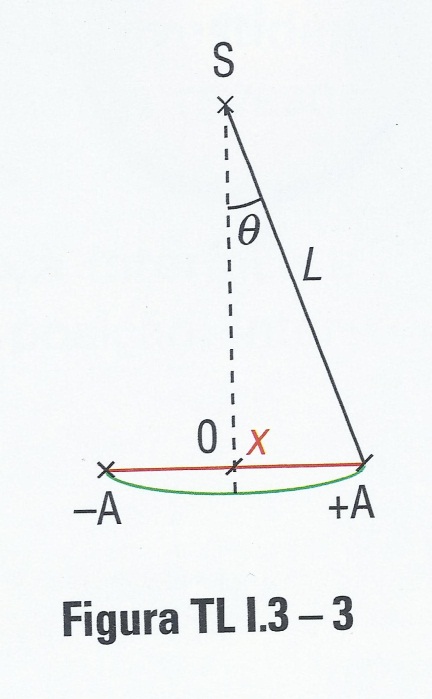

 

Dentro desta aproximação e de acordo com a figura 2,

(SI) assim  (SI), sendo   (SI) podemos escrever  (SI)

O módulo da aceleração, , é diretamente proporcional ao módulo do deslocamento, , em relação ao ponto O.

Deste modo o movimento é harmónico simples (MHS), com uma frequência angular de .

 

Como , obtém-se:

 

Assim na superfície da Terra () poderemos afirmar que o comprimento () de um pêndulo em metros é aproximadamente um quarto do quadrado do seu período em segundos: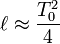  

 

Materiais Utilizados

 

. Balança digital | Valor de menor divisão =  | Precisão = ;

. Suporte universal;

. Digitímetro | Valor de menor divisão =  | Precisão =;

· Fotossensor;

· Fios de ligação;

. Craveira | Valor de menor divisão =  | Precisão =  | Alcance = ;

. Cronómetro analógico | Precisão =  | Valor de menor divisão = ;   

. Fio de nylon;

. Fita métrica | Valor de menor divisão =  | Precisão =  | Alcançe = ;

2 esferas metálicas

. Diâmetro (E1) =  |

. Diâmetro (E2) =  

 

. Massa (E1)= 

. Massa (E2)=;

. 2 nozes de laboratório;

. Transferidor | Valor de menor divisão = 10° | Precisão = 5° | Alcançe = 180°.

 

Procedimentos Experimentais

Utilizando o Digitímetro

1ª Parte

(a influência da amplitude das oscilações no período do pêndulo)

1. Mantivemos ao longo de todos os ensaios o mesmo oscilador  e o mesmo comprimento do pêndulo ().

2. Realizámos 5 ensaios para cada uma das 5 amplitudes de oscilação distintas (10°, 20°, 40°, 60°) relativas à posição vertical de equilíbrio.

3. Registo do tempo de passagem da esfera  pelo fotossensor e cálculos posteriores numa tabela.

 

2ª Parte

 

(confirmação do isocronismo nas oscilações de pequena amplitude)

1. Fizemos variar a amplitude das oscilações (não modificando o comprimento do pêndulo, ), mantendo-as sempre inferiores a 10° (). Sendo que para cada uma das amplitudes referidas foram realizados 5 ensaios.

2. Registo do tempo de passagem da esfera  pelo fotossensor () e cálculos posteriores numa tabela.

 

3ª Parte

(a influência do comprimento do pêndulo no período das oscilações)

1.  Mantivemos as pequenas oscilações ().

2. Determinámos o período das oscilações do pêndulo, agora para 2 comprimentos diferentes

 = e

 =).

Sendo que para cada um deles realizámos, de novo, 5 ensaios.

3. Representámos graficamente a função  e determinámos a equação da reta de ajuste (por regressão linear).

4. Calculámos, a partir do declive da reta, o valor da acelaração da gravidade.

5. Registámos os tempos obtidos de passagem da esfera  pelo fotossensor e os cálculos posteriores numa tabela.

 

4ª Parte

(a influência da massa no período do pêndulo)

1. Escolhemos para o comprimento do pêndulo um dos já utilizados ().

2. Substituimos a nossa esfera metálica inicial por uma do mesmo material mas mais leve e de menor volume ().

3. Determinámos o período de pequenas oscilações e compará-mo-lo com o período das oscilações do pêndulo inicial.

4. Registámos os tempos de passagem da esfera  pelo fotossensor e os cálculos posteriores numa tabela.

 

Resultados Experimentais

 

1ª Parte

 = 10°

Nº ensaio

∆t(s)

v/ms-1

T(s)

T(s)

1

6,0358×10-2

0,315

7,3

11,1

2

1,1588×10-1

0,164

14,0

3

9,0345×10-2

0,210

10,9

4

8,7555×10-2

0,217

10,6

5

1,0393×10-1

0,183

12,5

 

 = 20°

Nº ensaio

∆t/s

v/ms-1

T/s

T/s

1

3,4466×10-2

0,551

4,16

5,03

2

3,2832×10-2

0,579

3,96

3

6,1480×10-2

0,309

7,42

4

4,1054×10-2

0,463

4,95

5

3,8680×10-2

0,491

4,67

 = 40°

Nº ensaio

∆t/s

v/ms-1

T/s

T/s

1

1,4009×10-2

1,36

1,69

1,96

2

2,7859×10-2

0,68

3,37

3

1,2942×10-2

1,47

1,56

4

2,4094×10-2

0,79

2,09

5

9,003×10-3

2,11

1,09

 

 = 60°

Nº ensaio

∆t/s

v/ms-1

T/s

T/s

1

7,748×10-3

2,45

0,94

0,97

2

8,932×10-3

2,13

1,08

3

5,659×10-3

3,36

0,68

4

7,333×10-3

2,59

0,88

5

1,0420×10-2

1,82

1,26

 

 

Massa (E1) =

 

2ª Parte

 = 5°

Nº ensaio

∆t/s

v/ms-1

T/s

T/s

1

9,3910×10-2

0,202

11,4

12,3

2

1,0985×10-1

0,173

13,2

3

1,1244×10-1

0,169

13,6

4

8,8356×10-2

0,215

10,7

5

1,0382×10-1

0,183

12,5

 

 = 8°

Nº ensaio

∆t/s

v/ms-1

T/s

T/s

1

1,0321×10-1

0,184

12,5

12,2

2

1,0243×10-1

0,185

12,4

3

1,0084×10-1

0,188

12,2

4

1,0092×10-1

0,188

12,2

5

9,6358×10-2

0,197

11,6

 

 

 

Massa (E1) =

 

3ª Parte

Nº ensaio

∆t/s

v/ms-1

T/s

T/s

T2/s2

1

1,0321×10-1

0,184

12,5

12,2

148,8

2

1,0243×10-1

0,185

12,4

3

1,0084×10-1

0,188

12,2

4

1,0092×10-1

0,188

12,2

5

9,6358×10-2

0,197

11,6

 

Nº ensaio

∆t/s

v/ms-1

T/s

T/s

T2/s2

1

9,6632×10-2

0,197

8,0

9,9

98,0

2

1,2103×10-1

0,157

10,0

3

1,2999×10-1

0,146

10,8

4

1,3888×10-1

0,137

11,5

5

1,1319×10-1

0,168

9,3

 

 =

 

 =

Massa (E1) =

 

4ª Parte

Nº ensaio

∆t/s

v/ms-1

T/s

T/s

1

1,1705×10-1

0,158

9,9

10,2

2

1,2018×10-1

0,154

10,2

3

1,3149×10-1

0,141

11,1

4

1,2384×10-1

0,149

10,5

5

1,1031×10-1

0,168

9,3

 

3ª Parte

 

Nº ensaio

∆t/s

v/ms-1

T/s

T/s

T2/s2

1

1,0321×10-1

0,184

12,5

12,2

148,8

2

1,0243×10-1

0,185

12,4

3

1,0084×10-1

0,188

12,2

4

1,0092×10-1

0,188

12,2

5

9,6358×10-2

0,197

11,6

 

Nº ensaio

∆t/s

v/ms-1

T/s

T/s

T2/s2

1

9,6632×10-2

0,197

8,0

9,9

98,0

2

1,2103×10-1

0,157

10,0

3

1,2999×10-1

0,146

10,8

4

1,3888×10-1

0,137

11,5

5

1,1319×10-1

0,168

9,3

 =

 

 =

 

Massa (E1) =

 

4ª Parte

 

Nº ensaio

∆t/s

v/ms-1

T/s

T/s

1

1,1705×10-1

0,158

9,9

10,2

2

1,2018×10-1

0,154

10,2

3

1,3149×10-1

0,141

11,1

4

1,2384×10-1

0,149

10,5

5

1,1031×10-1

0,168

9,3

 

 

 

Massa (E2) =

 

Questões Pós-Laboratoriais

 

Servirá o relógio de pêndulo da mesma maneira na Terra e na Lua?

Na Lua o pêndulo oscilará mais lentamente do que na Terra pois a intensidade do campo gravitacional (g) é cerca de 6 vezes menor do que aqui. Portanto, dado que o período é inversamente proporcional à raiz quadrada da intensidade do campo gravitacional, o pêndulo oscilará cerca de 60,5 = 2,4 vezes mais lentamente do que aqui.

 

T = 2\pi\sqrt{\frac{L}{g}}

 

. T, período;

. L, comprimento do fio;

. g, acelaração gravítica

Caso o relógio fosse de pêndulo elástico (como era efetivamente os relógios de pulso Omega dos primeiros astronautas), a intensidade do campo gravitacional não teria qualquer influência, visto que a gravidade ao diminuir, diminui também o comprimento do fio mantendo assim o período (T) constante.

Que acontecerá a um relógio de pêndulo, cujo fio seja metálico, num dia muito quente?

Sabendo que com o calor os fios metálicos dilatam (os metais são excelentes condutores térmicos) o comprimento destes também irá aumentar, segundo a fórmula:

 

. \Delta L,\  variação do comprimento em metros (m);

. \alpha,\  coeficiente de dilatação linear em Kelvin  K^{-1} ;

. L_0,\  comprimento inicial em metros (m);

. \Delta T = T-T_0,\  variação de temperatura em Kelvin (K) ou em graus Celsius (°C).

 

Logo o periodo (T) irá aumentar visto que este é diretamente proporcional ao comprimento do pêndulo:

 

T = 2\pi\sqrt{\frac{L}{g}}

 

. T, período;

. L, comprimento do fio;

. g, acelaração gravítica.

 

Discussão de Resultados

Antes de mais importa salientar a inexistência de quaisquer problemas significativos aquando da medição dos resultados apresentados anteriormente.

Em relação à primeira parte da nossa atividade experimental é nos fácil verificar que quanto maior for a amplitude de oscilação menor será o seu período, isto para ângulos superiores ou iguais a 10° (10°, 20°, 40°, 60°). Por outro lado relativamente à fase seguinte constatámos que para pequenas oscilações (<10°) o período de oscilação é praticamente independente da amplitude do movimento, podendo assim ser considerado um Movimento Harmónico Simples (HMS). Para os dois ângulos aqui utilizados ( = 5° e  = 8°)  a diferença entre a média dos períodos de oscilação foi de 0,1 segundos, um valor extraordinariamente pequeno. Na terceira parte da atividade para além de termos verificado que para pequenas oscilações quanto maior for o comprimento do pêndulo maior será o período do movimento oscilatório (para um comprimento de fio de 25,00 cm obtivemos um período de 9,9 s, por outro lado quando utilizámos um fio com 36,50 cm resultou num período oscilatório de 12,2 s, assim comprovámos a influência do comprimento do fio no período do movimento harmónico simples do pêndulo), ainda tentámos, calcular um valor aproximado do da aceleração gravítica. Contudo obtivemos um valor extremamente desviado do real (, muito pouco exato), possivelmente devido ao reduzido número de ensaios para diferentes comprimentos de fio por nós efetuado, ou devido à baixa precisão do transferidor utilizado (Precisão = 5°), ou ainda devido à presença (inevitável) das forças de atrito atuantes no pêndulo que acabaram por aumentar ainda mais o tempo de passagem dos corpos pelo fotossensor (atritos estes, existentes no próprio ar). Ocorrera contudo, ainda, um outro imprevisto: não nos foi permitido utilizar comprimentos de fio superiores a 40 cm visto tratar-se da distância máxima do tampo da mesa ao topo do suporte universal (onde se encontrava pendurado o nosso pêndulo). Por último, ao substituirmos a esfera inicial por uma mais pequena e leve (mas mantendo o mesmo comprimento de fio, 25,00 cm), comprovámos, mais uma vez que para oscilações de reduzida amplitude, que o período do movimento oscilatório é independente da massa do oscilador (massa de

E1= 

e tem um período de 9,9 segundos já a massa de

E2 = 

e tem um período oscilatório de 10,2 segundos), uma diferença de períodos bastante reduzida.

 

Concluindo, atingimos praticamente todos os objetivos traçados, desde comprovar a influência do comprimento do pêndulo no valor do período, até, verificarmos que afinal a massa do oscilador para pequenas amplitudes era irrelevante para obtermos tal valor. 

__________________________________

Outros Trabalhos Relacionados

Ainda não existem outros trabalhos relacionados