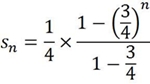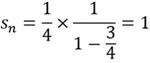|
Flatland – o país plano Quase toda a história se desenrola em “Flatland”, um mundo a duas dimensões; Os seres que o habitavam eram polígonos regulares; Em “Flatland” não se admitia a existência de outras dimensões; todos os defeitos eram atribuídos à irregularidade no ser; Um quadrado habitante de Flatland parte numa viagem à descoberta de outras dimensões; Dá-se conta da existência da dimensão zero, um, e três; O quadrado estabelece uma relação entre as diversas dimensões, tentando descobrir outras dimensões ainda para além da terceira; Um ponto desloca-se ao longo de um comprimento de nove centímetros, formando uma linha de nove centímetros, que se pode representar por 9.
Uma linha de nove centímetros percorre, paralelamente a si mesma, um comprimento de nove centímetros, formando um quadrado com nove centímetros de lado, que pode representar-se por 92.
Então, um quadrado, de nove centímetros de lado, deslocando-se paralelamente a si mesmo, formaria uma outra coisa de nove centímetros de lado, o cubo, representando-se por 93.
Pelo mesmo raciocínio, o quadrado queria ir em busca de outras dimensões, quando a sua ambição o levou de volta à flatland. Dimensões inteiras Relacionam-se: . Dimensão; . Número de caixas necessário para recobrir o objecto; . Tamanho dessas caixas.
Um ponto possui dimensão zero Uma superfície plana dimensão dois
Uma linha recta dimensão um Um sólido dimensão três. “Nuvens não são esferas, montanhas não são cones, continentes não são círculos, um latido não é continuo e nem o raio viaja em linha recta.“ O que é um fractal? A matemática dos fractais pode servir para explicar e caracterizar fenómenos e formas encontradas na natureza que não podem ser explicadas com a matemática convencional. Fractais são formas geométricas incapazes de serem classificados nos moldes da Geometria Euclidiana devido, principalmente a três características que os definem e distinguem de outras formas : auto-semelhança em diferentes níveis de escala, dimensão fractal e sua complexidade infinita. Geometria Fractal Actualmente a Geometria Fractal, e em especial a Dimensão Fractal, está a ser utilizada em diversas áreas do conhecimento, como o estudo de sistemas caóticos, caracterização de objectos, análise e reconhecimento de padrões em imagens, análise de texturas e medição de comprimento de curvas. Características dos fractais - auto-semelhança; - complexidade infinita;
- dimensão fractal Tipos de fractais: Fractais Geométricos: são aqueles que derivam da geometria tradicional através de funções iterativas a partir de uma figura inicial Exemplos: a curva de Peano, o Triângulo de Sierpinski etc.
Pirâmide de Sierpinsky Fractais Aleatórios: são aqueles gerados por computadores, resultantes de iterações, operadas num sistema não linear, de forma recursiva.
História dos fractais Euclides verificou que um grão de areia apresenta três dimensões (largura, altura e profundidade), enquanto que a superfície arenosa da praia é visualmente plana (com duas dimensões); O ponto de partida para Mandelbrot foi a questão de dimensão que escapou a Euclides; Mandelbrot acrescentou essa ideia de dimensão e surgiu a geometria dos fractais. Aplicações dos fractais na nossa vida Na Biologia - Estudo da influência da superfície irregular das proteínas nas iterações moleculares; Na Geografia - A descrição e caracterização de falhas sísmicas e terramotos são obtidos através do estudo de sua estrutura fractal; Na Computação - criação de softwares de compactação de imagens; criptografia, codificação e descodificação de áudio e vídeo; Na Medicina - Os campos mais desenvolvidos são o diagnóstico do cancro e das doenças cardíacas. Dimensão euclidiana e Dimensão Fractal Dimensão Euclidiana: . Apenas assume valores inteiros. . O valor da dimensão representa a dimensionalidade do espaço em que dado objecto está inserido; . Representa o espaço onde a forma está inserida; Dimensão Fractal: . Assume valores fraccionários. –Representa o nível de irregularidade de um fractal; . Quanto maior a irregularidade de uma forma, maior é a sua dimensão fractal. . Representa o nível de ocupação do espaço pela forma; A Dimensão Fractal
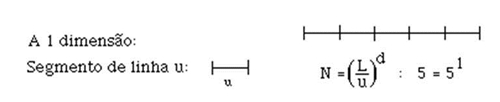
Temos: L = 1, N = 5 e u = 1/5
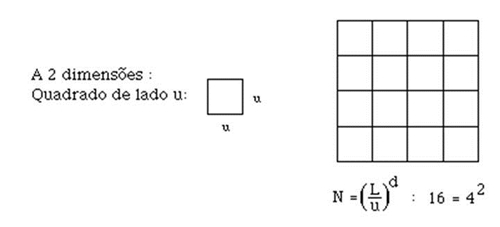
Temos: L = 1, N = 16 e u = (1/4)2
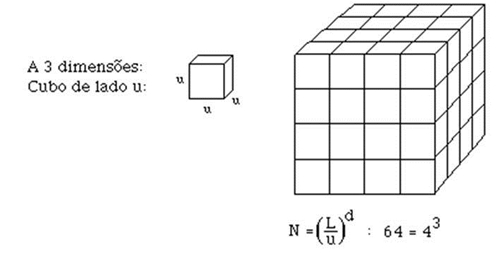
Temos: L = 1, N = 64 e u = (1/4)3 N = (L/u)^d d = log N log(L/u) Fractais cuja dimensão é assim calculada: Poeira ou Conjunto de Cantor
L = 1, N = 2 e u = 1/3: D = log2/log3 @ 0,6309... Curva de Koch
Tem-se L = 1, N = 4 e u = 1/3: D = log4/log3 @ 1,2618… Método da Contagem de Caixas O processo de contagem de caixas para a determinação da dimensão fractal.
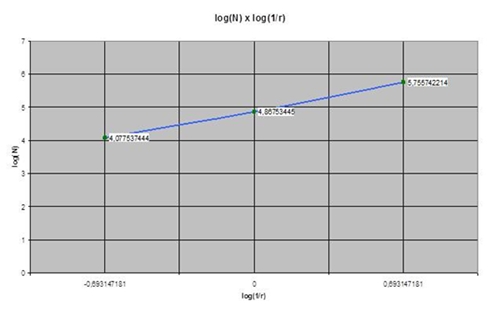
r = 0,5 mm | N = 316 r = 1 mm | N = 130 r = 2 mm | N = 59 Agora construamos o gráfico log(N) x log(1/r):
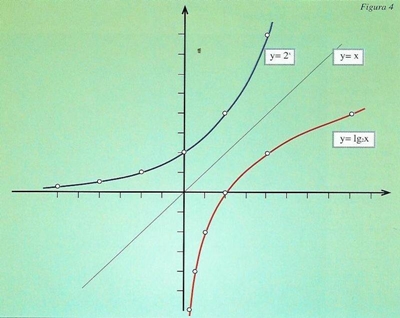
Gráfico auxiliar para a determinação da dimensão de um fractal Logaritmos e funções logarítmicas O que é uma função exponencial? Trata-se de uma função representada por uma potência cuja base b é constante e cujo expoente tem valor variável. Representa-se por: x y = bx O que é um logaritmo? Chamamos logaritmo de n de base b, e representamo-lo por logb n = a a um número a, tal que b elevado a a é igual a n, ou seja, ba = n
O que é uma função
logarítmica? Trata-se de uma função representada por um logaritmo cuja base b é sempre constante e a variável é o valor de x Representa-se por: Y = logb x Estabelecendo a relação directa, ba = n ↔ logb n = a
Calculando a função inversa de uma função afim, faríamos:
y = 3x + 2
↔ 3x = y - 2 ↔
x = y - 2 Então, calculando a inversa de uma função exponencial, faríamos : ba = n ↔ logb n = a
Sendo a função logarítmica a inversa da função exponencial.
x =
y - 2 ↔
y = x - 2 Sendo x a variável, e y a imagem. Teríamos que: ba = n ↔ logb n = a ↔ logb a = n
Habitualmente, efectua-se uma mudança de base de logaritmos para fazer os cálculos com a calculadora:
logb
x =
logb
x Exemplos de fractais O triângulo de sierpinsky
É de notar que: A área do triângulo de sierpinsky tende para zero, porque:
Supondo que a área do triângulo inicial é 1: 1ª figura: Área total dos buracos = 0 Área total do triângulo de Sierpinsky = 1 2ª figura:
Número de novos buracos: 1 Área de cada novo buraco = 1/4 Área total de novos buracos = 1/4 Área total de buracos = 1/4 Área colorida = 1 - (1/4) = 3/4 3ª figura:
Número de novos buracos: 3 Área de cada novo buraco = 1/4/4 = 1/16 Área total de novos buracos = 3 x (1/16) = 3/16 Área total de buracos = (1/4) + (3/16) Área colorida = 1 - (1/4) - (3/16) 4ª figura:
Número de novos buracos: 9 Área de cada novo buraco = 1/16/4 = 1/64 Área total de novos buracos = 9/64 Área total de buracos = (1/4) + (3/16) + (9/64) Área colorida = 1- (1/4) - (3/16) - (9/64) Portanto, a área dos buracos é dada por: 1/4 + 3/16 + 9/64 + 27/256 + ... Sendo an a sucessão da área dos novos buracos, an = (1/4) x (3/4)n-1 em que o primeiro termo, a1 = (1/4) e a razão r = 3/4 , sendo an uma progressão geométrica. Assim, a área total dos buracos será dada por:
Como (3/4)n tende para zero, a sucessão tende para:
Como a área total dos buracos tende para um, a área do triângulo de sierpinsky tende para zero. A área, an, do menor triângulo colorido é igual à área do menor buraco de iteração n, logo, a área do menor triângulo da iteração n é: an = (1/4)n Apesar da área do triângulo de Sierpinsky tender para zero, o perímetro total tende para: +∞ Supondo que o primeiro triângulo tem perímetro igual a 1, 1ª figura: 2ª figura: P = 1 P2 = 9 x (1/6) = 3/2 3ª figura: P3 = 27 x (1/12) = 9/4 = (3/2)2 Depois de uma iteração obtemos uma aproximação do triângulo de Sierpinsky com perímetro igual a 3/2 vezes o perímetro do triângulo original; Na iteração n o perímetro do triângulo fica (3/2)n -1 , porque o perímetro é uma progressão geométrica de razão 3/2 e primeiro termo igual a 1. Assim o perímetro tende para +∞ sempre que n tende para +∞ Sucessão do número de triângulos coloridos: a1 = 1 a2 = 3 a3 = 9 a4 = 27 an = 3 n-1 Sendo an uma progressão geométrica de razão r=3 e primeiro termo igual a 1. Sucessão do número de triângulos brancos a1 = 0 a2 = 1 a3 = 4 a4 = 9 an = a n-1 + 3 n-2 A Teoria do Caos Conhecer as leis que governam um sistema nem sempre significa conseguir prever a sua evolução. Há sistemas, chamados caóticos, que são bizarros e imprevisíveis, e que os físicos tentam estudar com a teoria do caos. Segundo esta teoria, uma das características dos sistemas caóticos é que uma diferença, ainda que mínima, das condições iniciais amplifica-se excessivamente e leva a evoluções completamente diferentes. Outros Trabalhos Relacionados
|
|




 Dividimos
Dividimos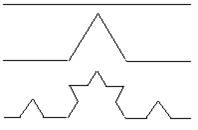 Cada
lado do triângulo é dividido,
continuamente, em três partes. Cada
triângulo formado é equilátero.
Cada
lado do triângulo é dividido,
continuamente, em três partes. Cada
triângulo formado é equilátero.