Teoria das Eleições, Teoria da Partilha, e Grafos

TEORIA DAS ELEIÇÕES

Introdução

Hoje em dia, vivemos num mundo desenvolvido e maioritariamente democrático onde todos têm direito a expressar a sua opinião, a tomar palavra em decisões que determinam o avanço dum país. Um mundo onde, resumidamente, todos os cidadãos, desde homens, mulheres e crianças, sem exclusão social por etnias, religião ou qualquer outro aspecto, têm iguais direitos e deveres perante a sociedade.

Assim nos encontramos muitas vezes face à necessidade de resolver questões referentes a toda uma nação, em que o conflito de opiniões não deixa claro a preferência da população. Recorremos então a uma eleição, um processo que nos indicará a preferência dos eleitores através do voto, onde cada elemento expressa secretamente a sua escolha.

Há vários sistemas de votação e de contagens dos votos, que se aplicam nas mais diversas eleições. Uma vez recolhidos os votos, procede-se ao seu tratamento e análise, afim de determinar o(s) vencedor(es). É deste estudo matemático que se ocupa a Teoria das Eleições.

Tipos de eleições

Em Portugal, a nível nacional, existem 7 tipos de eleições:

. Eleição para a Assembleia Constituinte

. Eleição Presidencial

. Eleição Legislativa

. Eleição Legislativa Regional

. Eleição Autárquica

. Eleição Europeia

. Eleição para o Conselho da Comunidade Portuguesa

Temos ainda voto em várias eleições a nível europeu e internacional, como por exemplo:

. Secretário-Geral da ONU

. Presidente da Comissão Europeia

. Deputados do Parlamento Europeu

Sistemas de Votação

. Maioritário

. Preferencial

. Aprovação

. Proporcional (Método de Hondt)

Sistema Maioritário

Boletim de Voto

No boletim de voto consta o nome de todos os concorrentes, e o eleitor deverá seleccionar apenas um consoante a sua preferência.

Exemplo:

Contagem

Maioria Simples

Numa única votação, é eleito o candidato com maior número de votos, independentemente dos outros resultados ou das percentagens obtidas.

Exemplo:

A – 237 votos

B – 192 votos

C – 242 votos

Vencedor: C

Maioria Absoluta

Numa primeira votação, é eleito o candidato que tiver metade dos votos mais um, pelo menos.

Se isto não suceder, procede-se a uma segunda votação.

Nesta segunda votação, pode-se proceder de duas diferentes maneiras:

. São submetidos apenas os dois candidatos mais votados, e forçosamente um será o vencedor (excepto em caso de empate, o que é muito improvável e até hoje nunca aconteceu).

. Refaz-se a votação, com todos os candidatos, mas a contagem dos votos é feita por maioria simples.

Aplicação

O sistema de maioria simples é utilizado, por exemplo, na eleição do Presidente da Junta de Freguesia ou da Câmara Municipal. A eleição por maioria absoluta, onde a segunda votação seria por maioria simples e novamente com todos os candidatos, é aplicada nalgumas comissões directivas da ONU, dos Jogos Olímpicos e clubes de futebol.

Sistema de Aprovação

Boletim de Voto

Neste procedimento, cada eleitor pode votar em tantos candidatos quantos quiser. Consoante a sua opinião, selecciona todos os candidatos que aprovar. O boletim tanto pode estar em branco, como ter um voto em todas as opções.

Exemplo:

Contagem

Cada candidato aprovado recebe um voto, sendo que nenhum eleitor pode votar duas vezes no mesmo candidato, e o que tiver mais votos ganha, independentemente dos outros ou de percentagens.

Aplicação e Vantagens

Este método é muito prático e facilmente compreensível, fomenta a adesão ao voto e permite que se façam escolhas mais flexíveis. É também dos mais justos, pois permite ver o verdadeiro valor de todos os candidatos, nomeadamente dos minoritários.

Aplica-se actualmente em diversas organizações, mais especificamente, por exemplo, na nomeação do Secretário-Geral das Nações Unidas.

Sistema Preferencial

Boletim de Voto

Neste terceiro sistema, não se trata da selecção de um ou mais candidatos, mas sim de os colocar por ordem preferencial, sem exclusão de nenhum.

Exemplo:

Contagem

O sistema preferencial, na contagem dos votos, subdivide-se em dois métodos: o de Borda, e o de Condorcet.

Tomemos como exemplo a seguinte situação:

Numa eleição para o delegado de turma, candidatou-se a Márcia (M), a Cláudia (C), o Henrique (H) e a Sandra (S).

Resolução segundo:

Método de Borda

Atribui-se x pontos a cada lugar (1º, 2º, 3º, …) por ordem decrescente, respectivamente. A contagem é feita consoante a quantidade de votos que um candidato teve nos vários lugares, e o vencedor será o que tiver mais pontos.

1º lugar: 4 pontos

2º lugar: 3 pontos

3º lugar: 2 pontos

1º lugar: 1 ponto

Márcia

5x1 + 4x3 + 8x1 + 10x3 + 1x2 = 57

Cláudia

5x3 + 4x4 + 8x4 + 10x2 + 1x1 = 84

Henrique

5x4 + 4x2 + 8x3 + 10x4 + 1x4 = 96

Sandra

5x2 + 4x1 + 8x2 + 10x1 + 1x3 = 43

Vencedor: Henrique

Método de Condorcet

Aqui se procede a um confronto directo, par a par, entre todos os candidatos, para se determinar o que vence mais vezes. Em caso de empate, não há vencedor.

Confrontos:

O Henrique venceu a todos os candidatos, logo foi o que obteve mais vitórias.

Vencedor: Henrique

Sistemas Proporcionais

Por vezes há eleições em que não se pretende encontrar um vencedor, mas sim distribuir mandatos entre os candidatos, através da conversão de votos.

Entre os sistemas de representação proporcional conhecemos os métodos de Hagenbach-Bischet e Sainte Lague, mas o mais conhecido e utilizado é o Método de Hondt.

Método de Hondt

Boletim de Voto

O boletim de voto deve ser preenchido de igual maneira ao de votação por maioria simples, marcando apenas o candidato que mais agrada ao eleitor.

Algoritmo

Para efectuar a conversão dos votos em mandatos…

. Faz-se a contagem dos votos apurados por cada candidato

. O nº de votos de cada um é dividido sucessivamente por 1, 2, 3, 4,…

. É marcado por ordem decrescente um número de quocientes equivalente ao número de mandatos que se pretende distribuir.

. Segundo os seus quocientes marcados, cada candidato terá a mesma quantidade de mandatos.

. Em caso de, na selecção do último mandato, haver dois ou mais quocientes iguais, o mandato é atribuído ao candidato com menor número de mandatos.

Exemplo:

Resultados:

Lista A – 4 mandatos

Lista B – 2 mandatos

Lista C – 2 mandatos

Lista D – 1 mandato

TEORIA DA PARTILHA

Introdução

É frequente confrontarmo-nos com situações em que é preciso fazer umas partilha equilibrada de algo, mas a sua divisão não ser facilmente óbvia.

São chamados casos discretos situações de objectos indivisíveis, como casas, carros, lugares no parlamento ou mobília.

Por outro lado, a divisão e partilha de bolos, pizas e somas de dinheiro, que são divisíveis de infinitas maneiras, equivalem aos casos contínuos.

Por vezes podemo-nos também deparar com um caso misto, com objectos tanto divisíveis como o contrário. Por exemplo, uma herança.

Partilhas no caso discreto

Foram vários os métodos estudados neste sistema de partilha de objectos indivisíveis, nomeadamente os de:

. Hamilton

. Jefferson

. Adams

. Webster

. Huntington-Hill

. Método da Marca

Os cinco primeiros têm a mesma base e aplicam-se com as mesmas noções (divisor padrão, quota padrão, quota arredondada), o que diferencia é o tipo de arredondamento que é feito.

Divisor Padrão:

É o quociente entre o total de sujeitos e o total de lugares ou objectos a atribuir.

Quota Padrão:

É o número de lugares a que cada Estado teria direito se pudesse receber um número não inteiro de lugares.

Podem-se fazer dois tipos de arredondamento:

Quota Inferior – o arredondamento é por defeito, portanto é igual ao maior número inteiro contido na quota padrão.

Quota Superior – o arredondamento é por excesso, pois se adiciona 1 valor ao maior número inteiro contido na quota padrão.

Método de Quota

Um método de partilha que atribui sempre a cada Estado um número de lugares igual à Q.S. ou à Q.I. chama-se Método de Quota. Quando isto não acontece diz-se que o método em questão viola a regra da quota.

Analisaremos apenas alguns com mais pormenor:

Método de Hamilton

Algoritmo:

. Calcular o Divisor Padrão.

. Calcular a Quota Padrão de cada Estado

. Atribuir a cada Estado a sua Quota Inferior, que corresponderá ao número de lugares a que cada um tem direito

. Se sobrarem lugares devem-se atribuir, um a um, aos Estados por ordem decrescente da parte decimal da sua Quota Padrão.

Exemplo:

A fábrica do Pai Natal estava a ficar uma enorme confusão, e assim decidiu que era necessário eleger membros dos diversos grupos e atribuir um cargo a cada um. Entre o administrador da secção dos brinquedos, o controlador de cores, o designer, o estilista do Pai Natal e outros, eram precisos 20 elementos, que seriam escolhidos consoante a importância quantitativa da sua classe.

Os companheiros do Pai Natal eram os seguites:

. Bolinhas de Pêlo falantes (para chapéus de Pai Natal) – 307

. Duendes – 284

. Renas (aprendizes e profissionais) – 227

. Fadas – 182

O ratinho Kiwiri encontrou os rascunhos das contas do Pai Natal:

Divisor Padrão = 1000/20 = 50

Nº cagos a distribuir:

Bolinhas de Pêlo: 6

Duendes: 6

Renas: 4

Fadas: 4

Método da Marca

Este método aplica-se sobretudo em divisões de herança, por exemplo, em que há um grupo de diversificados objectos, e o objectivo é fazer a partilha mais justa.

Algoritmo

. Numera-se e ordena-se os objectos, fazendo uma barra com a sucessão dos números por ordem.

. O primeiro jogador coloca duas marcas, entre as quais devem constar os objectos que prefere, sem alterar a ordem dos mesmos.

. Seguem-se os outros jogadores, efectuando o mesmo.

. O primeiro conjunto de objectos ( do início à primeira marca) é atribuído ao jogador cuja marca é a primeira.

. Os objectos que se encontrarão entre a segunda marca da barra e a seguinte do mesmo jogador, são atribuídos ao próprio.

. Todos os objectos que se encontrarem após a última marca pertencerão ao jogador restante.

. Entre os objectos sobrantes, pode-se refazer o método da marca ou sorteá-los.

Exemplo:

O Pai Natal quis oferecer também algumas prendinhas aos seus 3 ajudantes mais próximos. Para evitar preferências, comprou doze presentes e pediu ao duende, à rena e à fada que seguissem o método da marca para receberem os presentes.

Duende – jogador A

Rena – jogadora B

Fada – jogadora C

Duende (A) – segmento 1

Rena (B) – segmento 4-9

Fada (C) – segmento 11-12

Sobram as prendas 10,3 e 2, que poderão ser sorteadas.

Partilhas no caso contínuo

Para resolver problemas de partilha de casos contínuos, ou seja de objectos divisíveis, podemos aplicar um dos seguintes métodos:

. Divisão e Escolha

. Divisor Único

. Seleccionador Único

. Último a Diminuir

Método de Divisão e Escolha

É o mais simples dos métodos de partilha em casos contínuos. Entre dois jogadores, sorteia-se o divisor e o seleccionador.

Perante o objecto, o divisor divide-o no que considere serem duas partes iguais, e o seleccionador escolhe a que mais lhe agradar.

Método do Divisor Único

(exemplo com três jogadores)

. Sorteia-se um divisor, os outros todos farão a escolha.

. O divisor divide o objecto em três partes (P1, P2 e P3) que julgue serem iguais.

. Casos que poderão acontecer e soluções:

. Se um seleccionador escolher, por exemplo, P1 e P2, o outro seleccionador ficará com a parte que quiser e o divisor com a que sobrar.

. Se um seleccionador escolher P2, o outro P3, forçosamente o divisor terá P1.

. Se ambos os seleccionadores escolherem, por exemplo, P2, o divisor ficará com P1 ou P3 consoante a sua preferência. Das duas restantes, juntam-se de novo e um dos seleccionadores divide enquanto que o outro escolhe.

Método do Seleccionador Único

(exemplo com três jogadores)

. Sorteia-se um seleccionador e os restantes serão divisores.

. Um dos divisores divide o objecto em duas partes que acredite serem iguais, e o outro escolhe uma.

. Cada divisor divide a sua metade em três partes que considere iguais.

. O seleccionador escolhe uma das três partes dum divisor, e igualmente do outro.

. Cada jogador fica com duas sextas partes do objecto.

Método do Último a Diminuir

(exemplo com cinco jogadores)

. Todos os jogadores são seleccionadores e divisores, simultaneamente, e ordenam-se aleatoriamente.

. O primeiro jogador selecciona o que pense ser um quinto do objecto.

. O jogador que se sucede analisa a parte escolhida e:

*concorda que é corresponde a um quinto e passa a vez ao seguinte

* Julga que é maior do que um quinto, retira dessa parte o pedaço necessário e passa a vez de jogar ao seguinte.

. O terceiro jogador analisa novamente a parte escolhida, e segue o mesmo procedimento do que o seu antecessor, e assim sucessivamente.

. Quando todos os jogadores efectuarem este procedimento, é atribuída a parte seleccionada ao último jogador que a diminuiu.

GRAFOS

Introdução

Um grafo é um conjunto de vértices ligados por arestas, utilizados para simplificar a representação de um esquema, mapa, urbanização, … Afim de resolver problemas que neste se coloquem.

Um grafo pode ser conexo, se directa ou indirectamente houver uma ligação entre todos os pontos, ou desconexo, caso contrário. Assim como pode ter uma possível, mas não obrigatória, orientação.

Será completo se, sendo p o número de vértices do grafo, todos os vértices tiverem grau igual p -1. Ou seja, se todos os vértices estiverem ligados as todos os restantes.

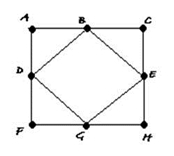
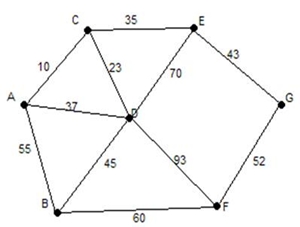
   Grafo Conexo                   Grafo Desconexo                  Grafo Completo                     Grafo orientado

Podemos ainda definir que um…

. Passeio é uma sequência de vértices e de arestas

. Trilho é um passeio em que todas as arestas são diferentes.

. Caminho é um passeio em que todos os vértices são distintos.

. Circuito é um trilho que começa e acaba no mesmo vértice.

Grafos de Euler

Leonard Euler (1707-1783), foi um dos génios da matemática, por ter produzido mais trabalhos do que qualquer outro matemático. Em matéria de grafos, partiu do problema de Konigsberg, e foi ele que deu o grande avanço neste âmbito. Assim se explica a presença do seu apelido nos circuitos e trilhos eulerianos.

Circuito de Euler

É um circuito que percorre todas as arestas de um grafo (sem repetições) e começa e acaba no mesmo vértice.

Um circuito de Euler só é admitido num grafo conexo, cujos vértices tenham todos grau par.

A partir do momento em que esta condição é cumprida, é possível encontrar rapidamente um circuito de Euler começando em qualquer vértice.

Exemplo:

Circuito de Euler:   A B C E B D G E H G F D A

Trilho de Euler

. É um trilho que, igualmente sem repetição, passa por todas as arestas dum grafo começando e terminando em vértices diferentes.

Só poderá ser admitido na existência de no máximo 2 vértices de grau ímpar.

Para encontrarmos um trilho euleriano num grafo, que cumpra esta condição, é necessário começar num dos vértices de grau ímpar e terminar no outro.

Exemplo:

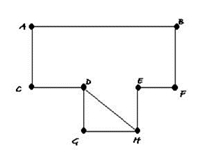
D e H são os únicos vértices de grau ímpar, assim devemos começar o trilho em D e terminar em H, ou o inverso.

Trilho de Euler:    D C A B F E H D G H

Eulerização

Se, por exemplo, for necessário efectuar um circuito ou trilho de Euler, mas o grafo tiver mais do que dois vértices de grau ímpar, é possível acrescentar arestas até chegar às condições necessárias para um circuito de Euler.

A este processo chamamos a “Eulerização”.

Exemplo:

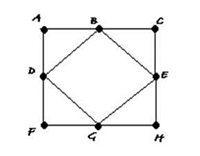
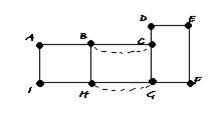
Neste grafo, os pontos B, C, G e H têm grau ímpar. Normalmente inicia-se num vértice ao acaso, e saltando sucessivamente para o seguinte acrescenta-se uma aresta quando se encontra um vértice de grau ímpar, até que todos os vértices tenham grau par.

Aqui, a maneira mais eficaz de eulerizar o grafo é interligar os vértices de grau ímpar, e uma vez que são quatro, acrescentamos apenas duas arestas:

B à C    e      H à G

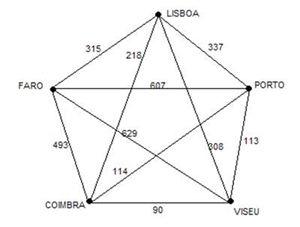
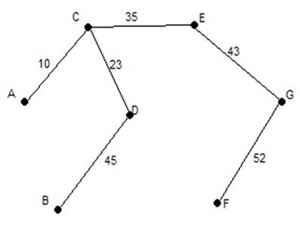
Assim obtemos um grafo onde todos os vértices têm grau par e já é possível efectuar um circuito de Euler.

Grafos de Hamilton

Sir William Hamilton (1805-1865) foi um matemático que muito contribuiu para descobertas desta ciência, nomeadamente da estatística, e é a este mesmo génio que devemos o nome do Circuito de Hamilton.

Circuito de Hamilton

É um caminho que começa e acaba no mesmo vértice, passando por todos e sem repetições.

Para problemas deste tipo, com o objectivo de encontrar a ligação mais curta, ainda se está a estudar uma resolução bem definida e universal, de maneira que os métodos utilizados actualmente são relativamente incertos e instáveis:

.  Método do Vizinho Mais Próximo

.  Método da Ligação do Custo Mínimo

NOTA: Num circuito de Hamilton, é condição necessária que o grafo seja completo.

Algoritmo do Vizinho Mais Próximo

. Escolher um dos vértices para ponto de partida.

. A partir desse vértice escolher a aresta com menor peso possível (se houver mais que uma escolher aleatoriamente)

. Continuar a construir o ciclo, partindo de cada vértice para um vértice não visitado segundo a aresta de menor peso.

. Do último vértice não visitado regressar ao ponto de partida.

Algoritmo da Ligação do Custo Mínimo

. Começar por escolher a aresta com menor peso, qualquer que seja.

. Escolher de seguida a aresta de menor peso como anteriormente, e assim sucessivamente com as seguintes restrições:

. Não permitir que se formem ciclos que não incluam todos os vértices

. Não permitir que 3 arestas, do ciclo que estamos a procurar, se encontrem no mesmo vértice.

Exemplo:

Segundo o

Vizinho mais Próximo…

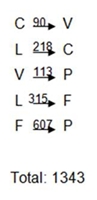
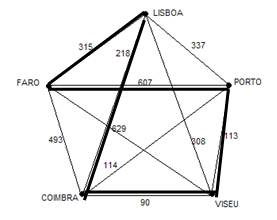
Neste método, para ter a certeza de que obtivemos o circuito mais leve, teríamos de descobrir todos os ciclos do grafo, pois ainda não há nenhuma equação que traduza o problema. 

Segundo a

Ligação do Custo Mínimo

O nº de ciclos num grafo, sendo n o

número de vértices, é igual a:

  (n-1)!     

2

Árvores

Uma árvore é um grafo conexo sem circuitos.

Uma árvore abrangente é um grafo que representa a ligação entre todos os pontos de um outro grafo, sendo esta directa ou indirecta, sem circuitos. Se for uma árvore abrangente mínima, apresentará a ligação com menos peso (mais curta, mais económica, …).

Grafo

Árvore

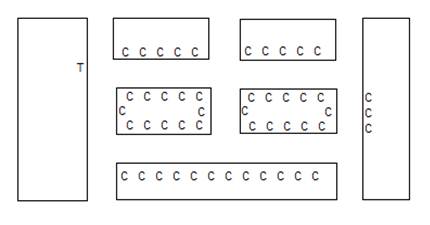
Algoritmo de Kruskal

Para encontrar a árvore mínima dum determinado grafo.

. Escolher as arestas com menor peso

. Nunca formar ciclos

Problema do Carteiro Chinês

O Problema do Carteiro Chinês deve o seu nome ao matemático Meigu Guan, que em 1962 levantou este tipo de problemas eulerianos com base na ideia de um carteiro a fazer a sua distribuição.

Exemplo:

As renas do Pai Natal precisam de uma hora de descanso na noite do dia 24, mas entretanto o trabalho não pode parar. No bairro das estrelinhas, o Pai Natal terá de distribuir as prendas a pé o mais rápido possível para poder pegar de novo no seu trenó. As casas estão dispostas da seguinte maneira:

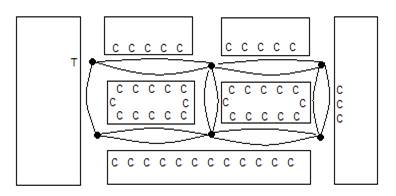
C – Casas

T – Trenó

O Pai Natal tem de percorrer o menor número de ruas que conseguir, tendo de passar por todas as que tiverem casas duas vezes (uma em cada passeio), e acabar e começar junto ao trenó.

O grafo adequado para este problema é o seguinte:

Este grafo tem dois vértices de grau ímpar, logo não seria possível efectuar um circuito de Euler. No entanto, o percurso mais curto, em que o Pai Natal só teria de percorrer duas vezes uma rua, é o seguinte:

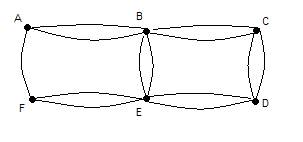
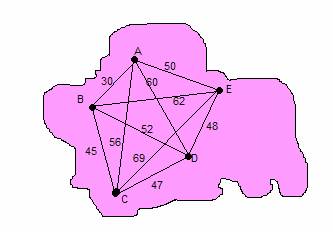
A B E B C D C B A F E D E F A

Problema do Caixeiro Viajante

O problema do Caixeiro Viajante é aquele em que se aplicam os circuitos de Hamilton. Os vértices são pontos cujas ligações estão devidamente valorizadas consoante a distância, custo, … O objectivo é percorrer todos os pontos uma só vez e terminar no ponto de partida.

Exemplo:

Oh não! Estão todos de volta ao Pólo Norte, as prendinhas já foram entregues! Os duendes estão descarregar o trenó, com sacos vazios e prendas que sobraram dos meninos mal comportados. “Oh não! Ainda aqui está uma caixa!”. Abriram-na e descobriram que se tinham esquecido de deixar um chocolate em cada casa! E agora? Já é muito tarde, e os meninos não podem abrir a prenda sem terem o seu bombom do dia de Natal…

Trabalho para todos: cada um vai ter de ir a um país entregar os bombons. Duendes, renas, fadinhas e o Pai Natal, ninguém pode ficar de braços cruzados!

Coube ao Rodolfo distribuir os chocolates na Terra Cor-de-Rosa, e aqui está o mapa que lhe deram, com as casas a percorrer, as ruas e as distâncias em metros:

 . Casas  _ Ruas

. Rodolfo, toca a fazer contas!

Segundo o:

Vizinho mais próximo:

Segundo a:

Ligação do Custo Mínimo:

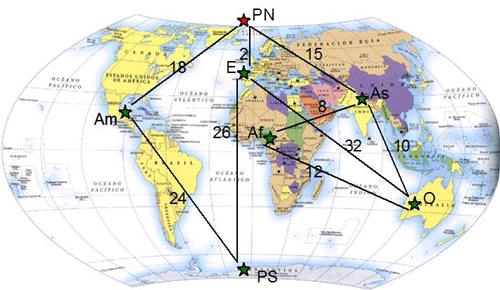
R: O percurso mais rápido para a rena é o apresentado em ambas as soluções, que corresponde a 220 metros.

Redes

As árvores abrangentes mínimas servem de solução a muitos problemas que englobamos num só tipo, as redes. Aplicadas nas mais diversas situações, desde a construção duma rede de cabos à ligação de cidades por estradas, com o apoio do Algoritmo de Kruskal.

Exemplo:

O Pai Natal, sensibilizado pelos problemas ecológicos e suas consequências, achou que fazer a separação do lixo não era suficiente para ajudar o ambiente. Olhou para o seu escritório, e ao ver-se deparado com pilhas e pilhas de cartas das crianças, percebeu a quantidade de papel desperdiçado ali estava!

Ora bem, é preciso agir. Adeus papel, e assim decidiu que modernizar-se um pouco e optar pela Internet como via de receber os pedidos simplificaria muito mais o problema.

Cada país já tinha a sua ligação de cabos de Internet por todas as cidades, e havia um computador por cada zona a que ligavam todas as nações mais próximas. Era ainda necessária criar uma ligação entre essas áreas e o computador do Pai Natal, na Lapónia (Pólo Norte).

No mapa estão assinalados os computadores, e os custos em Nataizz duma ligação Internet entre eles.

Am – América

E – Europa

As – Ásia

Af – África

O – Oceânia

PS – Pólo Sul

PN – Pólo Norte

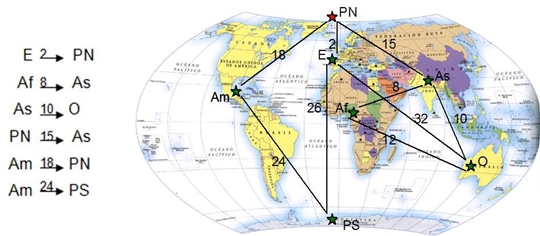
O duende Makimini fez ao Pai Natal o favor de ver que ligação seria mais económica, e foi este esquema que lhe apresentou:

FONTES

Fontes bibliográficas

Livros

"Matemática Aplicada às Ciências Sociais" Bloco 1, BRANCO Isabel, LONGO Elisabete, Texto Editora, 2004

"Matemática Aplicada às Ciências Sociais" Bloco 2, BRANCO Isabel, LONGO Elisabete, Texto Editora, 2005

Outros Trabalhos Relacionados