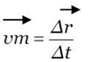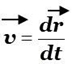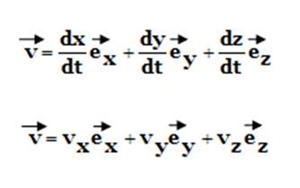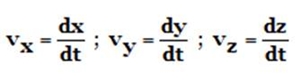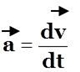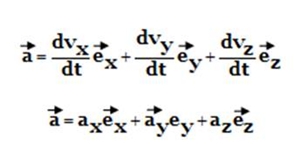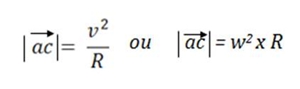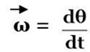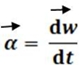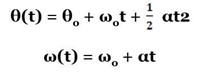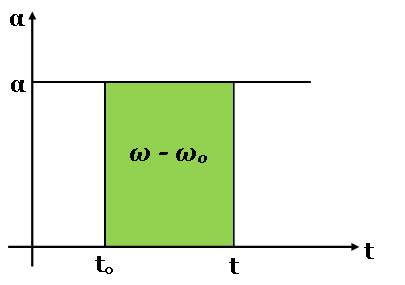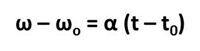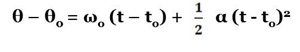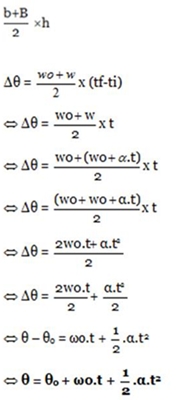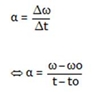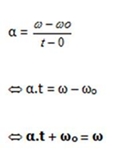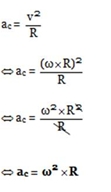Pressupostos

Inicialmente, tinha escolhido para o meu projecto o movimento rectilíneo uniforme, mas alterei-o, pois o movimento que tinha escolhido não iria promover uma aula tão interactiva com a turma, visto que é o movimento mais simples que estudámos o ano passado. Por isso, resolvi mudar para o movimento circular uniformemente acelerado, que vai ser uma matéria nova a estudar este ano.

Questões

1. Qual a posição do vector aceleração angular, α, em relação ao movimento?

2. A componente centrípeta da aceleração é constante?

3. A aceleração tangencial será constante?

Hipóteses

1. Suponho que o vector aceleração angular, terá o sentido do movimento quando este é acelerado e o sentido contrário ao do movimento quando este é retardado.

2. A componente centrípeta da aceleração será constante, se a força aplicada ao corpo for a mesma e for constante em módulo.

3. A aceleração tangencial é constante devido à variação do módulo da velocidade ser regular.

Fundamento Teórico

O movimento circular uniformemente acelerado, é um movimento onde uma partícula movimenta-se numa trajectória circular de raio R com aceleração tangencial constante. O movimento circular uniformemente variado possui velocidade variável e a aceleração angular constante e diferente de zero.

Características:

. A trajectória é uma circunferência.

.  A velocidade tangencial é variável em módulo, direcção e sentido e varia uniformemente.

. A aceleração tangencial é constante em módulo, mas é variável em direcção e sentido.

. A aceleração centrípeta é variável em módulo, direcção e sentido.

. A direcção e o sentido da velocidade, no movimento circular, são alterados a cada instante, em razão da acção da aceleração centrípeta.

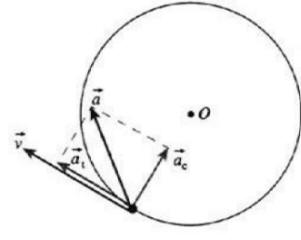
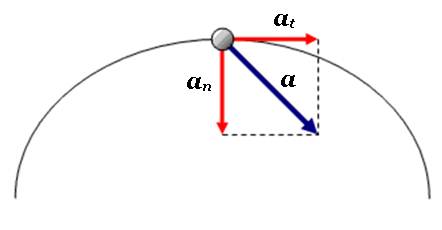
Fig.1 – Movimento Circular Uniformemente Acelerado.

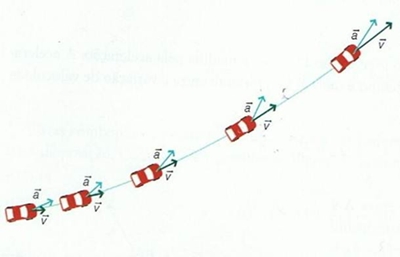
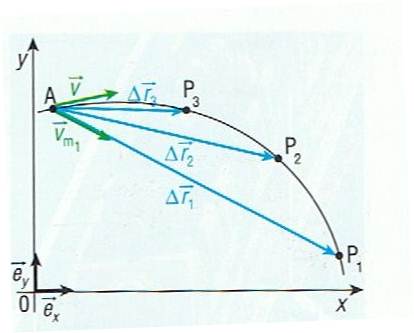
Fig.2 – Trajectória Curvilínea com movimento acelerado.

A figura acima mostra-nos uma trajectória curvilínea com movimento acelerado, sendo o vector velocidade sempre tangente à trajectória e a aceleração aponta sempre para o interior desta. A figura revela-nos que o movimento é acelerado, não só pelo aumento do módulo da velocidade, mas também pelo aumento da distância percorrida pelo carro em intervalo de tempos iguais.

Velocidade Média e Velocidade Instantânea

A velocidade média é o quociente entre o deslocamento e o correspondente intervalo de tempo:

Essa velocidade indica-nos se uma partícula muda mais ou menos rapidamente de posição num dado intervalo de tempo Δt. Como Δt tem sempre um valor positivo, a direcção e o sentido da velocidade média coincidem com os do deslocamento.
O módulo da velocidade, v = |v|, indica-nos a rapidez da partícula.

Sendo a velocidade um vector sempre tangente à trajectória, pode variar em módulo, em direcção ou simultaneamente em módulo e direcção.

Mas a descrição do movimento de uma partícula em termos da sua velocidade média não permite conhecer o que acontece em cada momento do seu percurso. Isso só é possível recorrendo à velocidade instantânea.

A velocidade instantânea, ou simplesmente velocidade, é igual ao limite para que tende o vector velocidade média, quando o intervalo de tempo tende para zero. A velocidade instantânea é pois, a taxa de variação do vector posição, r, por unidade de tempo, o que matematicamente corresponde à derivada do vector posição, r, em ordem ao tempo.

A velocidade é em cada instante tangente à trajectória, em cada ponto, e tem o sentido do movimento.

Se o vector posição, r, for expresso em função das suas coordenadas cartesianas, x, y e z, o vector velocidade instantânea, v, será dado por:

Onde v_x, v_y e v_z são as componentes cartesianas do vector velocidade, que correspondem às derivadas em ordem ao tempo das coordenadas cartesianas, x, y e z, de posição.

Fig.3 – Quando P se aproxima muito de A, Δt tende para 0 e a velocidade média dá lugar à velocidade instantânea.

Tab.1 – Características da trajectória curvilínea.

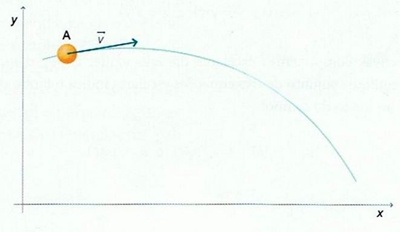
Fig.4 – Visualização do vector velocidade tangente à trajectória.

Aceleração

A aceleração instantânea, a, ou simplesmente aceleração, é uma grandeza física que permite conhecer a variação da velocidade em cada instante. A aceleração instantânea, é igual ao limite para que tende a aceleração média, quando o intervalo de tempo, tende para zero. Portanto, é igual à taxa de variação temporal da velocidade, o que, matematicamente, corresponde à derivada do vector velocidade, em ordem ao tempo.

Se o vector velocidade, v, for expresso em função das suas componentes cartesianas, v_x, v_y e v_z, o vector aceleração, a, será dado por:

Onde a_x, a_y e a_z são as componentes cartesianas do vector aceleração.
 

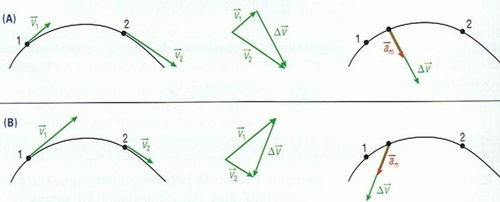
Fig.5 – Em (A) o movimento é acelerado e em (B) é retardado. Em qualquer um dos movimentos, a_m e Δv têm a mesma direcção e sentido e apontam para o interior da curva descrita pela partícula.

Aceleração Centrípeta e Tangencial

Sempre que um corpo se movimenta numa trajectória não rectilínea, age sobre ele uma força cujo efeito é alterar a sua direcção, para que o corpo em estudo possa percorrer a trajectória curvilínea. Essa força é chamada força centrípeta.

De acordo com a segunda Lei de Newton (Fr = m x a), essa força é capaz de proporcionar no corpo uma aceleração, e esta é sempre perpendicular ao vector velocidade e orientada para o centro da trajectória. Essa aceleração é chamada aceleração centrípeta ou normal. É esta que provoca a variação da direcção do vector velocidade.

O módulo da aceleração centrípeta é dado por:

Em que v é o vector velocidade, é tangente ao movimento, e R é o raio da trajectória circular.

A aceleração normal ou centrípeta é tanto maior quanto maior for a velocidade do corpo (ou ponto material) sobre o qual se aplica a força e quanto mais apertada for a curva (pequeno raio de curvatura).

Existe ainda uma força que actua na direcção da velocidade, a componente tangencial, F_t, como o nome indica, é tangente à trajectória e está relacionada com a variação do módulo da velocidade. Terá o sentido do vector velocidade se o movimento for acelerado e o sentido contrário se o movimento for retardado.

No movimento circular uniformemente variado, a aceleração tangencial é constante, porque o módulo da velocidade varia sempre da mesma forma nos mesmo intervalos de tempo.

Numa trajectória curvilínea, como a direcção da velocidade está sempre a mudar, a componente centrípeta nunca pode ser nula.

F_t = m x a_t

F_c = m x a_c

Como as componentes tangencial e centrípeta da aceleração têm, respectivamente, a direcção e o sentido das componentes tangencial e centrípeta da força resultante. Por isso, a aceleração é a soma vectorial das componentes tangencial e centrípeta:

E o módulo da aceleração é dado por:

Fig.6 – Decomposição da aceleração na sua componente tangencial (a_t) e na sua componente normal ou centrípeta (a_n).

Na figura 6, podemos ver que em cada ponto da trajectória, o vector aceleração, pode ser decomposto numa componente tangencial e numa componente normal (ou centrípeta) à trajectória.

Tab.2 – Aceleração tangencial vs. Aceleração normal.

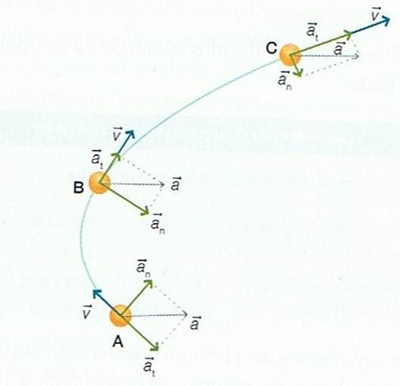
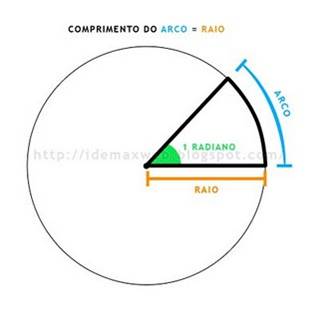
Fig.7 – Na posição A, verifica-se um movimento retardado, o vector aceleração tangencial opõe-se ao sentido do vector velocidade. Sendo nas posições B e C, movimento acelerado.

Quando o movimento é retardado, como no ponto A, o ângulo entre os vectores aceleração e velocidade é superior a 90º.

Quando o movimento é acelerado, como nos pontos B e C, o ângulo entre os vectores velocidade e aceleração é inferior a 90º.

O radiano

Considere uma circunferência de centro O e um arco AB nessa circunferência. Se o arco AB tem comprimento igual ao raio, dizemos que ele mede 1 radiano.

Portanto, radiano é a medida de um arco cujo comprimento é igual ao raio da circunferência que contém o referido arco. Como ao arco está associado um ângulo central, também podemos dizer que radiano é a medida do ângulo central que determina na circunferência um arco cujo comprimento é igual ao raio.

Fig.8 – radiano = raio/comprimento do arco.

Exemplo:  Para determinar a medida em radianos de um arco de comprimento igual a 12 cm, em uma circunferência de raio medindo 8 cm, fazemos:

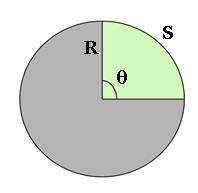
Portanto, m (AB) = 1,5 radianos.

O ângulo θ, que deve vir expresso em radianos, relaciona-se com a distância percorrida sobre a trajectória, S, através de:

Fig.9 – Relação da imagem com a fórmula ao lado.

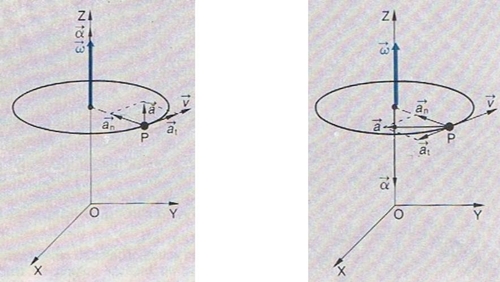
Tab.3 - Relação de ângulos em graus e m radianos.

Velocidade Angular

Para termos uma descrição sintética do movimento só nos falta uma grandeza indicando o eixo de rotação e o sentido da mesma a cada instante. Para isso criou-se um vector, ω , com direcção dada pelo eixo de rotação e sentido determinado pelo sentido em que é feita a rotação: para cima se o movimento é feito no sentido contrário ao dos ponteiros do relógio, para baixo no caso contrário. O módulo deste vector é dado a cada momento por:

Note-se que ao longo do tempo o sentido e o módulo da velocidade angular podem variar, bastando para isso que ao longo do movimento o sentido de rotação se altere e/ou a razão entre o ângulo percorrido e o tempo se vá alterando.

http://www.e-escola.pt/topico.asp?id=20#player2

 Fig.10 – No movimento acelerado, ω e α                        Fig.11 – No movimento retardado, ω e α
   têm o mesmo sentido e |ω| aumenta.                             têm sentidos contrários e |ω| diminui.

Aceleração Angular

De um modo geral define-se a aceleração angular de um corpo como sendo o quociente entre a variação da velocidade angular (Δω) e o intervalo de tempo em que ocorre essa variação de velocidade (Δt).

Esta definição é válida quando o intervalo de tempo considerado é grande e esta aceleração é designada mais correctamente por aceleração angular média.

Se se considerar um intervalo de tempo pequeno do corpo em estudo, a aceleração angular passa a ser definida como a razão entre a derivada da velocidade angular e a derivada em ordem ao tempo.

Esta aceleração denomina-se aceleração angular instantânea.
A aceleração angular mede-se em radianos por segundo ao quadrado, cujo símbolo é rad/s².

A aceleração angular pode ter valores positivos ou negativos. Se a velocidade angular aumentar em módulo, o movimento será acelerado e a aceleração angular terá o sinal da velocidade angular. Se a velocidade angular diminuir em módulo, o movimento será retardado e a aceleração angular terá sinal oposto ao da velocidade angular.

Se a aceleração angular tiver sempre o mesmo valor, o movimento circular será uniformemente variado. As variações do ângulo θ e da velocidade angular ω com o tempo têm então uma forma semelhante à variação da coordenada x e da velocidade v com o tempo num movimento rectilíneo uniformemente variado:

Gráficos

Gráfico 1 – aceleração angular

Do gráfico tiramos a informação que a aceleração angular é constante e positiva, e nos movimentos circulares uniformes esta é sempre constante. A área verde abaixo da recta da aceleração α e o eixo do tempo, representa a variação da velocidade angular.

Dada a aceleração angular podemos obter a variação de velocidade angular ω – ω₀ entre os instantes t₀ e t

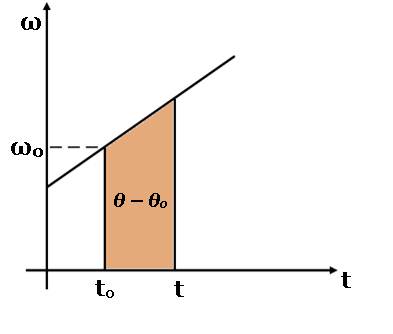
Gráfico 2 – velocidade angular

Dada a velocidade angular ω em função do tempo, obtemos o deslocamento θ – θ₀ do corpo entre os instantes t₀ e t, graficamente (área de um rectângulo + área de um triângulo).

Tab.4 – Leis do movimento.

O movimento é acelerado no sentido positivo quando, ω > 0 e α > 0, sendo acelerado no sentido negativo quando, ω <0 e α < 0. No entanto o movimento pode ser retardado também, sendo no sentido positivo quando, ω > 0 e α < 0 e retardado no sentido negativo quando, ω < 0 e α > 0.

Deduções

Através da área colorida (área de um trapézio), no gráfico 2 da página 12, conseguimos deduzir a seguinte fórmula:

área do trapézio:

Velocidade angular:

se α é constante no movimento circular uniformemente variado e t₀ = 0, então:

Aceleração centrípeta:

Equação de Torricelli:

Ligação do movimento numa situação em contexto real

Relativamente ao movimento que estou a estudar (movimento circular uniformemente acelerado), uma situação do contexto real que achei interessante abordar, foi a do “carrossel”, que há uns anos atrás existia muito nos parques infantis. Este carrossel, assim dizendo, só se move se for aplicada uma força, que normalmente é realizada pelos pais que empurram os filhos de modo a que o carrossel inicie o seu movimento circular. Quem exerce a força sobre o carrossel vai aplicá-la na sua componente tangencial, isto é, vai aplicar uma força, que irá ser responsável pela aceleração tangencial, que durante um curto espaço de tempo (enquanto o pai estiver a exercer a força), irá ser constante em módulo, mas irá variar tanto em direcção como em sentido. A aceleração tangencial irá ser responsável pela variação do módulo da velocidade, e quando o pai deixa de exercer a força essa mesma força, irá diminuir o seu módulo, passando a ser um movimento circular uniformemente retardado.

Esta situação aborda o movimento circular uniformemente acelerado. Isto acontece, enquanto o pai está a empurrar o carrossel para este rodar, e quanto maior for a intensidade da força aplicada maior será o módulo da velocidade. Pelo contrário, quando o pai deixa de aplicar a força, o carrossel irá diminuir o módulo da velocidade, passando a movimentar-se num movimento circular uniformemente retardado, até posteriormente vir a parar. Esta situação acontece devido à força de atrito e à resistência do ar que actuam sobre o carrossel.

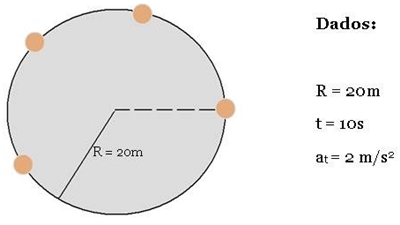
      Fig.12 – Pais a “empurrarem” o carrossel                                 Fig.13 – Carrosse

Exercício Resolvido

Com o meu movimento, não consegui encontrar nenhuma actividade experimental que já tivesse dados com que eu pudesse trabalhar as fórmulas deste movimento. Por esse motivo, não consegui realizar a parte experimental que está na estrutura do projecto, sendo assim vou colocar um exercício resolvido que aborda as fórmulas do meu movimento, de modo a “substituir” a parte experimental.

Um objecto inicia o seu movimento, a partir do repouso, deslocando-se numa trajectória circular de raio igual a 20m. A sua aceleração tangencial tem módulo de 2 m/s².

O objecto movimenta-se no sentido anti-horário. Após, 10 segundos.

Determine:

a) módulo da velocidade tangencial.

b) a aceleração angular.

c) a velocidade angular.

d) o comprimento do arco que o objecto percorreu durante os 10s.

e) ângulo θ percorrido.

f) a aceleração centrípeta.

g) a aceleração total e qual é a sua direcção.
 

a)  V_t = a x t
Û V_t = 2 x 10 = 20 m/s

b)  a_t = constante = 2 m/s²

a_t = α x R

Û α = at/R

Û α = 2/20 = 0,1 rad/s²

c)  ω (t) = ωo + α.t

Û ω (t) = 0 + 0,1 + 10

Û ω (t) = 1 rad/s

d)  s (t) = s_o + v_to.t + 1/2 .a_t.t²

Û s (t) = 0 + 0 + 1/2 .a_t.t²

Û s (t) = 1/2 x 2 x 10²

Û s (t) = 100m

e)  θ (t) = θo + ωo.t + 1/2 .α.t²

Û θ (t) = 0 + 0 + 1/2 .α.t²

Û θ (t) = 1/2 x 0,1 x 10²

Û θ (t) = 5 rad ou 286,5º

Cálculos Auxiliares

π rad                180º

5 rad                  x

x = 286.5º

f)  a_c = v²/20

Û a_c = 20²/20

Û a_c = 20 m/s²

g)  a_total =
Û a_total =
Û a_total = 20,1 m/s²

tg (β) = at/ac

Û tg (β) = 2/20

Û tg (β) = 0,1

tg^-1 (0,1) ≈ 5,7º

       ou

π rad                        180º

                                         x = 0,10 rad

x                               5,7º    

Assim, em t = 10s, o objecto:

a) Terá uma velocidade de 20 m/s.

b) A sua aceleração angular é de 0,1 rad/s².

c) Terá uma velocidade angular de 1 rad/s.

d) Terá percorrido uma distância de s = 100m.

e) Estará na posição θ = 5 rad ou 286,5º.

f) A sua aceleração tangencial é de 2 m/s².

g) A aceleração total é de 20,1 m/s² e faz um ângulo de 0,10 rad com a direcção radial, apontando para o centro da trajectória.

Conclusão

No início do meu projecto coloquei algumas questões e dei algumas hipóteses de resposta a estas. Depois de ter terminado todo o projecto cheguei à conclusão que uma das hipóteses de resposta que dei a uma das perguntas está incorrecta.

Isto é, o vector aceleração angular, α, será um vector perpendicular ao plano Oxy da trajectória circular e terá a mesma direcção da velocidade angular.

Relativamente, às outras questões colocadas, a hipóteses que coloquei estão correctas, por exemplo, para a questão 2, a aceleração centrípeta existe devido a uma força que tem direcção radial, a força centrípeta, sendo esta constante. A aceleração centrípeta também será constante, como se comprova com a fórmula: F_c = m.a_c, (um corpo com massa m com força centrípeta constante).

Quanto à aceleração tangencial, esta será constante no movimento circular uniformemente acelerado, devido à variação do módulo da velocidade ser regular ao longo de todo o movimento. Uma vez que a aceleração tangencial é a derivada temporal do módulo do vector velocidade, e a variação do módulo do vector velocidade é regular, então o módulo do vector velocidade sofre as mesmas variações no mesmo intervalo de tempo.

Posteriormente, à realização deste projecto fiquei a conhecer este novo movimento. Durante a realização deste projecto deparei-me com algumas dificuldades. No entanto consegui superá-las.

Outros Trabalhos Relacionados