Home » Ensino Médio » 2º Ano » Matemática » Probabilidade

Probabilidade

Todos os trabalhos publicados foram gentilmente enviados por estudantes – se também quiseres contribuir para apoiar o nosso portal faz como o(a) Sydney Pamplona e envia também os teus trabalhos, resumos e apontamentos para o nosso mail: geral@notapositiva.com.

Resumo do trabalho

Trabalho acadêmico sobre o tema 'Probabilidade' realizado para a disciplina de Matemática do 2º ano do Ensino Médio...

---

PROBABILIDADE

Probabilidade é o estudo das chances de se obter o resultado de um experimento aleatório. A essas chances são atribuídos os números reais do intervalo entre 0 e 1. Resultados mais próximos de 1 têm mais chances de ocorrer. Além disso, a probabilidade também pode ser apresentada na forma de percentual.

Um experimento aleatório pode ser repetido inúmeras vezes e nas mesmas condições e, mesmo assim, apresenta resultados diferentes. Cada um desses resultados possíveis é chamado de ponto amostral. Alguns exemplos de experimentos aleatórios são:

• Cara ou coroa (Lançar uma moeda e observar se a face voltada para cima é cara ou coroa). Há 50% de chance de aparecer um dos dois;
• Lançamento de dados (Lançar um dado e observar qual é o número da face superior também é um experimento aleatório). Há 6 chances para 1 número ser apresentado;
• Retirar uma carta aleatória de um baralho (Cada carta tem a mesma chance de ocorrência cada vez que o experimento é realizado, por isso, esse é também um experimento aleatório).

COMO CALCULAR A PROBABILIDADE

Para calcular a probabilidade podemos determinar os eventos e os resultados possíveis.

Por exemplo: Um recipiente contém 4 bolinhas azuis, 5 vermelhas e 11 brancas. Se uma das bolinhas for tirada do recipiente aleatoriamente, qual a probabilidade de que ela seja vermelha?

Escolher uma bolinha vermelha será o evento, e o número de resultados possíveis será igual à quantidade total de bolinhas no recipiente, ou seja, 20. Vale lembrar que os resultados possíveis é o nosso ponto amostral, representado por ômega (Ω).

Agora notamos que há 5 bolinhas vermelhas no recipiente, então o nosso número de eventos será igual a 5, enquanto a quantidade de resultados possíveis continua sendo 20, pois é o total de bolinhas. Colocando esses dados em prática, faremos uma divisão onde a Probabilidade será igual ao Número de Eventos dividido pelos Resultados Possíveis: 5/20 = ¼, entre 0 e 1 resultará em 0,25 e na forma de percentual 25%. Fórmula – P = n(E)/n(Ω)

APLICAÇÕES NA MATEMÁTICA

1. (ENEM-MEC) Em um blog de variedades, músicas, mantras e informações diversas, foram postados “Contos de Halloween”. Após a leitura, os visitantes poderiam opinar, assinalando suas reações em “Divertido”, “Assustador” ou “Chato”. Ao final de uma semana, o blog registrou que 500 visitantes distintos acessaram esta postagem.

O gráfico abaixo apresenta o resultado da enquete.

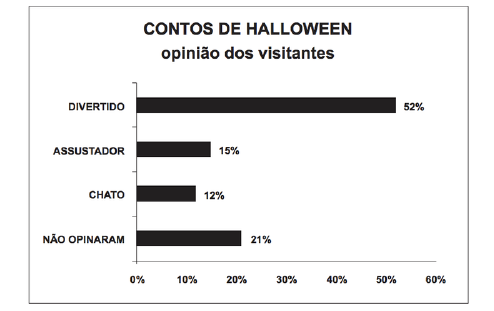
O administrador do blog irá sortear um livro entre os visitantes que opinaram na postagem “Contos de Halloween”.

Sabendo que nenhum visitante votou mais de uma vez, a probabilidade de uma pessoa escolhida ao acaso entre as que opinaram ter assinalado que o conto “Contos de Halloween” é “Chato” é mais aproximada por:

a) 0,09 b) 0,12 c) 0,14 d) 0,15 e) 0,18

Resolução:

O sorteio será feito apenas com os que opinaram (79%), podemos dizer que esse é o nosso evento, enquanto o ponto amostral é (100%). P = 79/100, P = 0.79. Multiplicando a probabilidade dos que opinaram pelo total de visitantes, obtemos: 0.79 * 500 = 395 visitantes que opinaram.

A probabilidade de quem votou “Chato” é de: P = 12/100, P = 0.12. Multiplicando a probabilidade dos que opinaram “Chato” pelo total de visitantes que opinaram, obtemos:

0.12 * 500 = 60. Podemos dizer que temos 60 eventos, enquanto o ponto amostral é 500.

P = 60/395, P = 0.15.

Alternativa D

2. (ENEM-MEC) Rafael mora no Centro de uma cidade e decidiu se mudar, por recomendações médicas, para uma das regiões: Rural, Comercial, Residencial Urbano ou Residencial Suburbano. A principal recomendação médica foi com as temperaturas das “ilhas de calor” da região, que deveriam ser inferiores a 31 °C. Tais temperaturas são apresentadas no gráfico:

Escolhendo, aleatoriamente, uma das outras regiões para morar, a probabilidade de ele escolher uma região que seja adequada às recomendações médicas é:

a) 1/5 b) 1/4 c) 2/5 d) 3/5 e) 3/4

Resolução:

De 4 possíveis lugares, apenas 3 tem a temperatura abaixo de 31 °C. Em fração ficaria ¾.

Alternativa E

3. Ao realizar uma prova objetiva em que cada questão possuía 5 alternativas de respostas, sendo apenas uma correta, um aluno decidiu assinalar aleatoriamente a resposta da última questão por falta de tempo. Qual é a probabilidade de esse aluno acertar a questão? E de errar?

Resolução:

De acertar:

n(E) = 1, n(Ω) = 5

P = 1/5 ou 20%

De errar:

n(E) = 4, n(Ω) = 5

P = 4/5 ou 80%

REFERÊNCIAS

SILVA, Luiz. Definições Básicas de Probabilidade. Disponível em: <http://mundoeducacao.bol.uol.com.br/matematica/definicoes-basicas-probabilidade.htm>. Acesso em: 02/12/17.

WikiHow. Como Calcular Probabilidades. Disponível em: <https://pt.wikihow.com/Calcular-Probabilidades>. Acesso em: 03/12/17.

SOUZA, J. Novo olhar - Matemática: 2 ed. São Paulo: Editora FTD S.A., 2013. Boas

 

Autores

WELLEN SALLY, SYDNEY LOPES PAMPLONA, MARIANA DA SILVA CRUZ, LUCAS DOS SANTOS ALVES, RAFAEL FERNANDES

91 Visualizações 12/09/2019

---