Fibonacci e as Sequências Matemáticas

Cláudia Viegas

Escola

Escola Secundária 3EB Dr. Jorge Correia

Fibonacci e as Sequências Matemáticas

Todos os trabalhos publicados foram gentilmente enviados por estudantes – se também quiseres contribuir para apoiar o nosso portal faz como o(a) Cláudia Viegas e envia também os teus trabalhos, resumos e apontamentos para o nosso mail: geral@notapositiva.com.

Resumo do trabalho

Trabalho sobre a teoria dos números e a evolução do conceito de número, particularmente sobre Fibonacci e as suas Sequências Matemáticas, realizado no âmbito da disciplina de Matemática (11º ano).

INTRODUÇÃO

O Tema central do nosso trabalho é a “Teoria dos números e a evolução do conceito de número”, deste tema geral o subtema que iremos abordar mais aprofundadamente irá ser “Fibonacci e as Sequências Matemáticas”.

“O conhecimento dos números foi fundamental na evolução da História do Homem. Desde as épocas mais remotas, têm chegado até nós vestígios que provam a sua importância. Hoje, os números estão presentes em qualquer actividade do Homem, desde a mais simples até mais complexa. Na vida do Homem não existe nada que não esteja de qualquer modo associado, ainda que de forma não evidente, aos números e ao seu conhecimento.” In Introdução do Plano do Trabalho entregue pelo professor

Os objectivos deste trabalho são de uma forma geral conhecer a origem e as sequências numéricas e suas propriedades. Isto é vamos com este trabalho apresentar a vida de um famoso matemático Italiano e as suas descobertas da matemática na Natureza. Quando se relaciona matemática com Natureza temos obrigatoriamente de falar dele e da sua famosa sequência numérica.

Elé é mesmo intitulado por mágico dos números devido à sua célebre sequência utilizada hoje em dia em inúmeras coisas mesmo até na programação dos computadores, para além da Natureza e do nosso corpo.

Vamos também fazer a relação da sequência com o número de ouro.

Para a realização deste trabalho, pretendemos recolher informações na Internet, em livros e etc, e organizá-la. Em formato papel e em formato digital. Em papel para ser entregue ao professor e em digital para apresentar à turma/ comunidade escolar.

BREVE BIOGRAFIA DE LEONARDO FIBONACCI E O SEU CONTRIBUTO PARA A MATEMÁTICA

Leonardo de Pisa (fig.7), nasceu em Pisa na Itália no ano 1175 e faleceu no ano 1250 também em Itália. Ficou conhecido por Fibonacci, devido ao facto de Fibonacci ser um diminutivo de fillius Bonacci, que queria provavelmente dizer filho de Bonacci, pois o seu pai chamava-se Guglielmo dei Bonacci.

As funções do seu pai estavam de certa forma relacionadas com transacções comerciais, viajava, frequentemente, para o Norte de África (actual Argélia). Leonardo, que o acompanhava nessas viagens, teve oportunidade de aprender a língua Árabe. Desde cedo começou a encontrar interesse nas técnicas de comércio, especialmente pelo cálculo, aprendendo estes assuntos com matemáticos e Islâmicos.

Mais tarde tornou-se mercador, actividade que, associada ao posto pela descoberta de manuscritos, o levou à Sícilia, ao Egipto e à Grécia.

Quando regressou à Itália, e na sequência de relações que tiveram com os árabes, escreveu em 1202, a obra Algebra e Almuchabila (título retirado da obra de Al-Khwarizmi), conhecida frequentemente pelo nome de Liber Abaci. Foi neste livro que Fibonacci introduziu o conceito dos números de Fibonacci e da sucessão de Fibonacci. O Liber abaci inicia-se com a ideia de que a aritmética e a geometria são interligados e se auxiliam mutuamente; no entanto, ele trata muito mais de números que de geometria, descrevendo primeiro as nove cifras indianas, juntamente com o símbolo 0, chamado zephirum em árabe. Explica métodos de cálculo com números inteiros e frações, cálculo de raízes quadradas e cúbicas, resolução de equações lineares e quadráticas, tanto pelo método de falsa posição como por processos algébricos. As raízes negativas e imaginárias não são admitidas. Há aplicações envolvendo permuta de mercadorias, sociedades e geometria mensurativa.

Esta obra de Leonardo de Pisa tornou-se de tal modo conhecida, que o próprio imperador, Frederico II (1194 – 1250) se deslocou a Pisa, em 1225, para se encontrar com ele e organizar um concurso matemático, em que Leonardo venceu. O título Liber Abaci, que se refere a cálculo numérico, está desajustado do conteúdo da obra de Leonardo onde, para além do cálculo, são tratadas questões de aritmética e álgebra.

Escreveu depois " Pratica Geometriae ", onde analogamente descreve as suas recolhas sobre Geometria e Trigonometria, contendo entre outras coisas, uma prova de que as medianas de um triângulo se dividem na razão de dois para um e uma analogia tridimensional do Teorema de Pitágoras.

Mas Fibonacci não foi apenas um compilador, pois estes livros contêm muitos exemplos não encontrados em documentos árabes.

Difundiu nos seus livros, os saberes matemáticos de origem indiana e árabe e estudou as operações elementares, assim como os números naturais, a decomposição de números em factores primos, as fracções e as equações entre outros.

Mas a concepção que Fibonacci apresentou no seu livro Liber abacci conhecido agora como os Números de Fibonacci foi o que mais o popularizou entre os outros matemáticos da sua época.

Fibonacci foi uma matemático excepcional e sua exposição da numeração indo-arábico foi importante no processo de transmissão destes, mas somente no século dezesseis o seu uso tornou-se comum.

SEQUÊNCIAS NUMÉRICAS

Os números são universais; são uma linguagem que transcende países e tempo.

A Sequência de Fibonacci consiste numa sucessão de números definindo os dois primeiros números da sequência como 0 e 1. Os números seguintes serão obtidos pela soma dos seus dois antecessores:

1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144,...

E assim sucessivamente.

Esta é a sequência de Fibonnaci.

Pode ser definida exponencialmente:

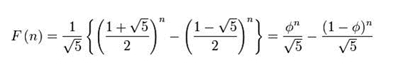
Ou pode ser dada pela fórmula:

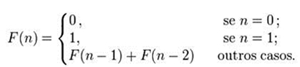
Ou ainda pode ser definida de forma recursiva. Isto quer dizer que é uma equação baseada nos seus valores anteriores.

Dados quinze termos consecutivos de uma sequência tipo Fibonacci a soma dos primeiros treze é igual a diferença entre o décimo quinto e o segundo termo.
A soma de dez termos consecutivos quaisquer de uma sequência tipo Fibonacci é onze vezes o sétimo termo da sequência considerada.

O NÚMERO DE OURO

Os Gregos determinaram a razão entre a diagonal do pentágono regular e o seu lado (quociente dourado) e concluíram que

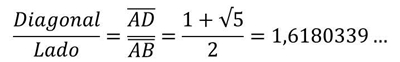
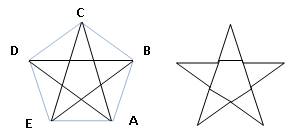
A este número chamaram número de ouro.

O NÚMERO DE OURO E A SEQUÊNCIA DE FIBONACCI

Se dividirmos cada um dos números da sequência pelo seu antecedente:

F₂/F₁=1; F₃/F₂=2; F₄/F₃=1,5; F₅/F₄=1,6(6); F₆/F₅=1,6 e se continuarmos assim sucessivamente, obtemos a seguinte sequência de números:

1,000 000; 2,000 000; 1,500 000; 1,666 666; 1,600 000; 1.625 000; 1,615 385; 1,619 048; 1,617 647; 1,618 182; 1,617 978; 1,618 056; 1,618 026; 1,618 037; 1,618 033; …

F_n+1/F_n aproxima-se cada vez mais do número de ouro.

O número de ouro tem o valor de ᵠ = (1+) /2 (=1,6180339…)

A designação adoptada para este número, f (Phi maiúsculo), é a inicial do nome de Fídias que foi escultor e arquitecto encarregado da construção do Pártenon (fig. 8), em Atenas.

A contribuição de Fibonacci para o número de ouro está relacionada com a solução do seu problema dos coelhos publicado no seu livro Liber Abaci, a sequência de números de Fibonacci.

DEMONSTRAÇÃO DA SEQUÊNCIA

Esta sequência foi descrita para descrever o crescimento de uma população de coelhos.

O objectivo era responder à seguinte questão: Quantos pares de coelhos é que vão existir daqui a um ano?

Condições:

No primeiro mês temos um coelho macho e um coelho fêmea. Estes dois coelhos acabaram de nascer.
Um coelho só atinge a maturidade sexual ao fim de um mês.
O período de gestação de um coelho dura um mês.
Ao atingirem a maturidade sexual, a fêmea irá dar à luz todos os meses.
A mãe irá dar todos os meses um coelho macho e um coelho fêmea.
Os coelhos nunca morrem.
Ao fim de um ano, Fibonacci concluiu que:
- Mês #0 - No início da experiência existe apenas um par de coelhos.
- Mês #1 – Após um mês, os coelhos acasalaram mas ainda não deram à luz (portanto existe somente um par de coelhos).
- Mês #2 – Neste mês já a fêmea deu à luz um par de coelhos. Existem agora dois pares de coelhos.
- Mês #3 – Depois de 3 meses, o par inicial de coelhos dá à luz mais um par de coelhos. No entanto, o segundo par acasala. Isto faz então um total de três pares.
- Mês #4 – Aos 4 meses, o par original tem mais um par de coelhos. O par nascido no mês #2 também dá à luz. O par de coelhos nascido no mês #3 acasalam, mas ainda não dão à luz. Isto faz um total de cinco pares....

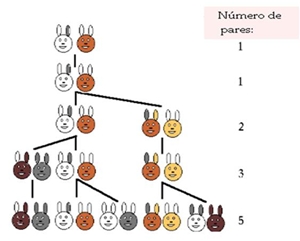
http://www.educ.fc.ul.pt/icm/icm99/icm41/suc-fib.htm

Concluindo, o número de pares de coelhos em determinado mês, é a soma dos pares de coelhos existentes nos dois meses anteriores a este.

Matematicamente, temos: F_n= F_n-1+ F_{n-2 ,n natural} → Sequência de Fibonacci

APLICAÇÕES NA NATUREZA

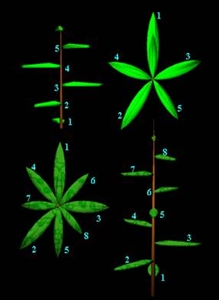
Os números de Fibonacci ligam-se facilmente à natureza. É possível encontrá-los no arranjo das folhas do ramo de uma planta, nas copas das árvores ou até mesmo no número de pétalas das flores (fig. 1).

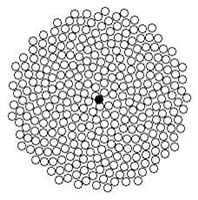
Os números de Fibonacci também podem ser vistos na organização das sementes na coroa das flores (fig. 2).

Pode também ser encontrado frequentemente em muitas outras formas vegetais: as folhas das cabeças das alfaces, a couve-flor, as camadas das cebolas ou os padrões de saliências dos ananases e da pinhas.

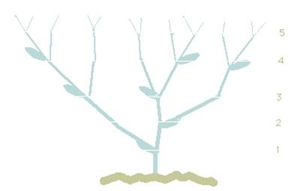
Uma planta em particular, mostra os números da sucessão de Fibonacci nos seus "pontos de crescimento". (fig. 3)

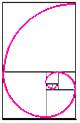
Se unirmos os quartos de circunferência de todos os quadrados vamos obter uma espiral, chamada Espiral de Fibonacci (fig. 4).

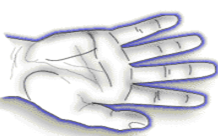
Muitas flores têm 5 pétalas, nós temos 2 mãos, cada uma com 5 dedos e cada dedo divido em 3 partes (fig.5):

O ananás tem 8 diagonais num sentido e 13 no outro.

As margaridas têm geralmente 34, 55 ou 89 pétalas (fig.6).

Vemos a sequência de Fibonacci numa alcachofra a florir, ou nas escamas de uma pinha. Podemos usa-la para explicar a reprodução dos coelhos. À medida que n se aproxima do infinito, a razão entre a (n) e a (n-1) aproxima-se de fi, o número de ouro – 1,618033989 – que foi utilizado para construir o Parténon e aparece nas composições de Bartók e Debussy

CONCLUSÃO

Todos os objectivos deste trabalho foram atingidos, de uma forma geral conhecer a origem e as sequências numéricas e suas propriedades . Apesar de termos pensado que estaríamos um pouco limitados no que toca à informação disponível, tal não aconteceu, visto que se encontrou importante informação tanto na Internet, como em diversos livros.

É maravilhoso chegar-se à conclusão que uma simples sequência de números faz parte de inúmeras coisas que nos rodeiam, desde a reprodução ideal dos coelhos até à formação das pétalas das flores.

Importante referir que a sequência de Fibonacci foi um grande auxílio para a construção de grandiosos monumentos da antiguidade e diversas outras coisas.

Este trabalho ajudou-nos a compreender que a matemática, quer queiramos, quer não, está presente nas nossas vidas a cada segundo. Aliás, a matemática acompanha-nos (podemos observar a sequência de Fibonacci nos dedos, nas mãos, etc), a matemática faz parte da nossa formação, da nossa vida. É como se esta ciência fosse a chave responsável pela abertura deste esplêndido universo.

Em suma, deixamos esta pergunta em aberto:

Seria possível haver vida sem matemática?

BIBLIOGRAFIA/NETGRAFIA:

[No Website] Sucessão de Fibonacci; [Modificado a] não indentificado; [Artigo Intitulado] Vários; [Consultado em] 28 de Abril de 2011 ; [No site] http://www.educ.fc.ul.pt/icm/icm99/icm41/index.htm

[No Website] Wikipédia; [Modificado a] 10 de Março de 2011; [Artigo Intitulado] Leonardo Fibonacci; [Consultado em] 28 de Abril de 2011 ; [No site] http://pt.wikipedia.org/wiki/Leonardo_Fibonacci#A_Sequ.C3.AAncia_de_Fibonacci

[No Website] não identificado; [Modificado a] não identificado; [Artigo Intitulado] O número de Ouro; [Consultado em] 1 de Maio de 2011 ; [No site] http://www.educ.fc.ul.pt/icm/icm99/icm17/ouro.htm

[No Website] Imática; [Modificado a] 29 de Janeiro de 2003; [Artigo Intitulado] Leonardo de Pisa; [Consultado em] 1 de Maio de 2011 ; [No site] http://www.ime.usp.br/~leo/imatica/historia/fibonacci.html

[Autor ]PICOULT, Jodi; [Titulo] No seu mundo; [Editora] Editora Civilização; [Local] Porto ; [Data da Publicação] 2010; [Páginas Consultadas] 270 e 271

[Autor ]ESTRADA, Maria Fernada, et al; [Titulo] História da Matemática; [Editora] Universidade Aberta; [Local] Lisboa ; [Data da Publicação] 2000; [Páginas Consultadas] 451, 452 e 453

[Autor ] NEGRA, Cristina e MARTINHO, Emanuel; [Titulo] Sem Limites – Matemática A 10ºAno; [Editora] Santillana Constância; [Local] Carnaxide, Lisboa ; [Data da Publicação] 2007; [Páginas Consultadas] 20