
O teu país
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod

Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod
Todos os trabalhos publicados foram gentilmente enviados por estudantes – se também quiseres contribuir para apoiar o nosso portal faz como o(a) Rita Laranjeira e envia também os teus trabalhos, resumos e apontamentos para o nosso mail: geral@notapositiva.com.
Trabalho sobre a vida e obra de Fibonacci, bem como apresentar a sucessão de Fibonacci e suas propriedades matemáticas, realizado no âmbito da disciplina de Matemática (11º ano).
Com este trabalho, concluído no dia 11/05/2011, para a disciplina de matemática a do 11ºano, iremos descrever brevemente a vida e obra de Fibonacci, bem como apresentar a sucessão de Fibonacci e suas propriedades matemáticas, dando a conhecer alguns factos interessantes da natureza relacionados com o tema.
Para entrega à professora, optámos por utilizar o programa de computador Microsoft Word, enquanto que para a exposição, optámos por utilizar o programa Power-Point.
Leonardo de Pisa, mais conhecido simplesmente por Fibonacci, foi um matemático italiano que nasceu por volta de 1180. É considerado por alguns como o mais talentoso matemático ocidental da Idade Média.
Por seu pai ter sido um abastado mercador pisano, Leonardo teve a oportunidade de viajar por várias regiões, nomeadamente o Oriente e o Norte de África desde muito pequeno, privilégio que lhe deu a possibilidade de observar os sistemas numéricos utilizados nessas regiões (numeração hindu-árabe) e que posteriormente introduziu na Europa, por ter reconhecido que a aritmética, com algarismos arábicos, era mais simples e eficiente do que com os algarismos romanos.
Ao longo das suas viagens, teve contacto com a obra de al-Khwarismi, de onde assimilou numerosas informações aritméticas e algébricas que compilou no seu primeiro livro “Liber Abaci”, cuja obra teve uma enorme influência para a introdução do sistema de numeração hindu-árabe.
Foi neste livro que Fibonacci introduziu o conceito dos números de Fibonacci e da sucessão de Fibonacci, tema principal do nosso trabalho.
 Posteriormente, escreveu “Pratica Geometriae” onde analogamente descreve as suas recolhas sobre Geometria e Trigonometria.
Posteriormente, escreveu “Pratica Geometriae” onde analogamente descreve as suas recolhas sobre Geometria e Trigonometria.
Difundiu nos seus livros os saberes matemáticos de origem indiana e árabe e estudou as operações elementares, assim como os números naturais, a decomposição de números em factores primos, as fracções, as equações, entre outros. No entanto, a concepção que Fibonacci apresentou no “Liber Abaci”, conhecido agora como os números de Fibonacci, foi o que mais o popularizou entre os outros matemáticos da sua época.
Pensa-se que Fibonacci terá morrido no ano 1250 em Pisa.
No século XIX, uma estátua foi erguida em Pisa, em sua homenagem. Hoje, está localizada na galeria ocidental do Camposanto, cemitério histórico da Piazza dei Miracoli.
Antes de iniciarmos o nosso tema principal, teremos que dar a definição de sucessão para dar a compreender, mais especificamente, a sucessão de Fibonacci. Uma sucessão de números reais é toda a função real de variável real natural, de domínio |N, que se pode definir através de uma expressão designatória ou de uma fórmula de recorrência (matéria de matemática actual).
A Sucessão de Fibonacci consiste numa sucessão de números, tais que, definindo os dois primeiros números da sequência como 0 e 1, os números seguintes serão obtidos por meio da soma dos seus dois antecessores. Portanto, os números são: 0,1,1,2,3,5,8,13,21,34,55,89,144,233,...
Analiticamente, a sequência de Fibonacci é dada pela seguinte fórmula:
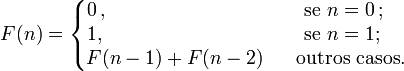
Embora a sucessão de Fibonacci se represente frequentemente por: F(n)=F(n-1)+F(n-2), n ∈ N, existem diversas fórmulas e propriedades relacionadas com esta sucessão, como as que apresentarei de seguida:
A soma dos quadrados dos números de Fibonacci é igual a un.un+1 → (u1)2+(u2)2+(u3)2+...+(un-1)2+ (un)2=un.un+1
O triângulo de Pascal também se relaciona com esta sucessão. Para podermos ver como, temos que primeiro explicar como se constrói o triângulo de Pascal:
Para se saber um determinado número, basta somar os dois números imediatamente acima deste.
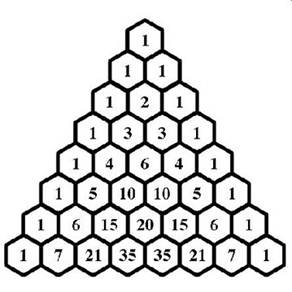
Mas como é que é possível encontrar os números de Fibonacci no triângulo de Pascal?
Analiticamente, é através das seguintes fórmulas:
f(n) = ![]() OU f(n) =
OU f(n) = ![]()
Por observação, podemos concluir empiricamente que a diagonal é realmente a soma dos números de Fibonacci:
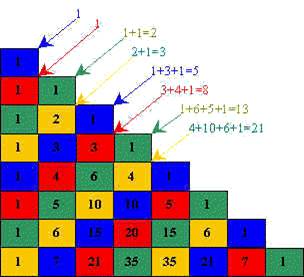
Também existem algumas propriedades interessantes relativamente aos múltiplos dos números de Fibonacci:
Se reparar, F(3), F(6), F(9), F(12), ...F(3k), k ∈ N, são múltiplos de dois.
F(4), F(8), F(12),..., F(4k), k ∈ N e (F(4k)=3), são múltiplos de três.
Isto sugere que F(5k) seja múltiplo de cinco (F(5)=3); F(6k) é múltiplo de oito (F(6)=8) e por aí fora.
Assim, podemos afirmar que:
O k-ésimo número de Fibonacci é múltiplo de F(k);
F(nk) é múltiplo de F(k), k ∈ N.
Vamos ver ainda como se pode obter uma espiral de Fibonacci.
Se reparar nos desenhos em baixo, as espirais por eles representadas são formada por, neste caso, seis quadrados (poderiam ser mais, infinitos até). O quadrado seguinte é sempre determinado pelo rectângulo anterior. Se reparamos no rectângulo temos que:
12+12+22+32+52+82+132 = 13×21
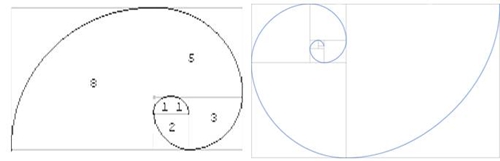
Pode-se então deduzir:
12+12+22 +...+F(n)2 = F(n)×F(n+1), n ∈ N ∧ n > 1
Podemos também encontrar a sucessão de Fibonacci relacionada com o número de ouro.
O número de ouro é um número irracional misterioso e enigmático que nos surge numa infinidade de elementos da natureza na forma de uma razão, e cujo valor é j = ( 1 + Ö 5 ) / 2 (= 1,618 033 989...)
Se dividirmos cada um dos números de Fibonacci pelo seu antecedente, reparamos que essa razão vai tender para o número de ouro. Isto é, se fizermos F2/F1=1; F3/F2=2; F4/F3=1,5; F5/F4=1,6(6); F6/F5=1,6 e assim sucessivamente.
Analiticamente, temos: Fn+1/Fn → j(Phi)
Nesta parte do nosso trabalho, vamos concentrar-nos no problema dos coelhos, problema inicialmente introduzido por Fibonacci no Liber Abaci. Assim, ele criou um cenário imaginário com as condições ideais (em baixo apresentadas), sob as quais os coelhos se poderiam procriar.
O objectivo deste problema era responder à seguinte questão:
Ao longo de doze meses, quantos coelhos serão gerados a partir de um único casal?
Condições:
Demonstrando, logicamente, temos: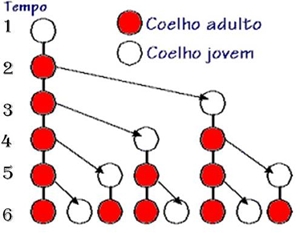
. Mês 0 → um par de coelhos, acabados de nascer, como descrito nas condições criadas por Fibonacci;
. Mês 1 → um par de coelhos, que já acasalou mas ainda não deu à luz, pelo período de gestação durar um mês;
. Mês 2 → dois pares de coelhos, o par de coelhos inicial e suas crias;
. Mês 3 → três pares de coelhos, o par de coelhos inicial, suas novas crias e o par de coelhos nascido no mês 2 que acasalaram, mas ainda não deram à luz;
. Mês 4 → cinco pares de coelhos, o par de coelhos inicial, suas novas crias, o par de coelhos nascidos no mês 2 e suas respectivas crias e o par de coelhos nascido no mês 3.
Como podemos facilmente reparar, a sequência dos números de pares de coelhos corresponde à sucessão de Fibonacci (1,1,2,3,5,8,13,21,34,55,89,144,…).
Concluindo, u(12) vai ser igual à soma dos seus dois antecessores.
Analiticamente, temos:
Fn = Fn-1+Fn-2 , n ∈ N
Os números de Fibonacci relacionam-se facilmente à natureza. É possível encontrá-los no arranjo das folhas do ramo de uma planta, nas copas das árvores ou até mesmo no número de pétalas das flores. Podemos também encontrar a espiral de Fibonacci nas sementes das flores, em frutos e pinhas.
Arranjo das folhas: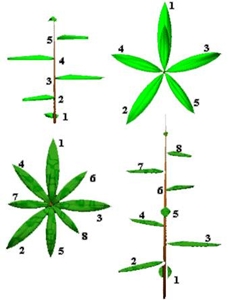
Como podemos observar na figura em baixo, os arranjos das folhas de algumas plantas em torno do caule são números de Fibonacci. Com este arranjo, todas as folhas conseguem apanhar os raios solares de igual forma e quando chove, o escoamento da água torna-se também mais fácil. Também podemos encontrar a sucessão de Fibonacci nos nossos próprios dedos das mãos!
Na planta do topo, contamos três rotações no sentido dos ponteiros do relógio, antes de encontrarmos a folha na mesma direcção da primeira. Passamos por cinco folhas, até que isso aconteça. Se contarmos no sentido contrário aos ponteiros do relógio, precisamos de duas rotações.
Na planta em baixo, para encontrarmos a folha na mesma direcção da primeira tem de se fazer cinco rotações no sentido dos ponteiros do relógio. Passamos por oito folhas até que isso aconteça. Se contarmos no sentido contrário aos ponteiros do relógio, precisamos de três rotações
Ramificações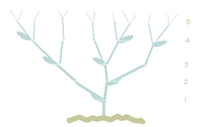
Quando a planta tem um novo rebento, leva dois meses a crescer até que as ramificações fiquem suficientemente fortes. Se a planta ramifica todos os meses, depois disso, no ponto de ramificação, obtemos uma figura semelhante à do lado direito.
Uma planta que cresce de forma semelhante a esta é a espirradeira ou cevadilha.
Dedos da mão:
Para encontrar a sucessão de Fibonacci, peço-lhe que olhe para a sua mão.
Consegue ver:
Para além dos objectivos posteriormente apresentados na introdução (pág.1), também concluímos com este trabalho que Leonardo Fibonacci não fora um mero compilador, como muitos comentadores mal-informados pensam.
Descobrimos também que a sucessão de fibonacci, tema principal do nosso trabalho, tem várias propriedades matemáticas, bem como diversos aspectos da natureza relacionados com a sucessão.
Google → www.google.com
Sucessão de Fibonacci → http://www.educ.fc.ul.pt/icm/icm99/icm41/
Leonardo Fibonacci → http://pt.wikipedia.org/wiki/Leonardo_Fibonacci