
O teu país
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod

Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod
Todos os trabalhos publicados foram gentilmente enviados por estudantes – se também quiseres contribuir para apoiar o nosso portal faz como o(a) Manuel Martins e envia também os teus trabalhos, resumos e apontamentos para o nosso mail: geral@notapositiva.com.
Resumo/Apontamentos sobre Argumentação e lógica formal, primeira parte da matéria da disciplina de Filosofia (11º ano).
A lógica é a disciplina filosófica que estuda a distinção entre argumentos válidos e inválidos, tendo em conta um conjunto de regras já existentes.
Um argumento é o modo de exteriorização do raciocínio, que é uma operação mental bastante complexa e consiste em relacionar juízos entre si, extraindo conclusões.
Como já foi abordado no ano anterior, o juízo é uma operação mental pouco complexa que nos permite relacionar conceitos, estabelecendo relações de conveniência ou de não conveniência.
O argumento é constituído por três proposições: duas premissas e uma conclusão.
Ex:
Todos os alunos responsáveis são pontuais
O João é pontual
O raciocínio relaciona proposições, que, por sua vez, relacionam conceitos. Deste modo, pode-se afirmar então o conceito é o elemento básico do discurso.
Ex: Vejo um objecto com as seguintes características: pequeno; serve para ver as horas, vermelho.
Comparando as características deste objecto, com as características de um conjunto de objectos com características semelhantes, pode-se dizer que esse objecto é um relógio. Para dizer isto, baseei-me no conceito que tenho de relógio, abstraindo-me das características não comuns desse objecto, em relação ao conjunto de objectos (neste caso, o facto do relógio ser vermelho e metálico. Como é lógico, nem todos os relógios são vermelhos e/ou metálicos; porém, todos eles servem para ver as horas).
Algumas características do conceito:
Um conceito pode ser objectivo, caso o seu termo se refira a um objecto material. Caso o termo se refira, por exemplo, ao amor, como é imaterial, dita-se que são conceitos espirituais. Existem ainda os conceitos funcionais, isto é, aqueles que estabelecem relações entre outros conceitos (ex: verbos, pronomes, conjunções, etc.)
A extensão de um conceito é o conjunto de seres, coisas e membros a que esse conceito se aplica. A extensão poder ser formada, por exemplo, por todos os Homens.
A compreensão de um conceito é o conjunto de qualidades, propriedades e características que definem esse conceito. Assim, a compreensão refere-se a características como: alto, magro, bonito, feio, grande, pequeno, etc.
A extensão e a compreensão variam na razão inversa; deste modo, à medida que aumenta a extensão, diminui a compreensão, e vice-versa.
1-Observação
2-Comparação das características semelhantes
3-Abstracção das características não comuns
4-Generalização – aplicação a todos os objectos da mesma espécie.
Operação mental que permite estabelecer relações de conveniência ou de não conveniência entre conceito, formando proposições, que podem ser classificado segundo a sua veracidade. Uma proposição é constituída por:
Nota: nem todas as frases são proposições. Apenas os enunciados que atribuem, declaram ou constatam alguma coisa, sendo portanto, passíveis de ser considerados verdadeiros ou falsos, é que se enquadram na categoria das proposições.
As proposições podem ser:
Dentro das proposições categóricas, Aristóteles estabeleceu quatro diferentes tipos, tendo em conta a sua qualidade e quantidade. A qualidade refere-se ao carácter afirmativo ou negativo, enquanto que a quantidade se refere à extensão do sujeito da proposição.
Se combinarmos a quantidade com a qualidade, pode-se distinguir quatro tipos de proposições:
Quadrado lógico da oposição:
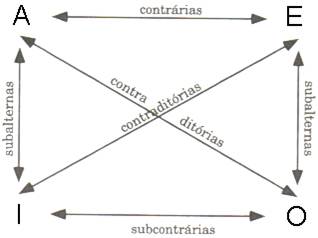
Lei das Inferências por Oposição
Regra das (Sub)Contrárias – Duas proposições contrárias não podem ser ambas verdadeiras;
Regra das Contraditórias – Duas proposições contraditórias não podem ser nem verdadeiras nem falsas ao mesmo tempo;
Regra das Subalternas – Duas proposições subalternas podem ser simultaneamente verdadeiras e simultaneamente falsas, bem como uma verdadeira e outra falsa.
Qualquer enunciado pode ser transformado em proposições categóricas na sua forma canónica.
Ex1: Ser filósofo é ser honesto = Todos os Filósofos são honesto (Tipo A)
Ex2: Todos os animais não são agressivos = Nenhum animal é agressivo (Tipo E)
Ex3: Existem arquitectos que são turcos = Alguns arquitectos são turcos (Tipo I)
Ex4: Nem todos os sábios são tolerantes = Alguns sábio não são tolerantes (Tipo O)
A verdade e a validade não se aplicam aos termos, visto que estes apenas se referem ao campo do possível.
Por outro lado, as proposições podem ser classificadas segundo a sua veracidade, porque consistem na predicação de um sujeito. Deste modo, quando a atribuição de uma determinada característica a um determinado sujeito corroborar a realidade, a proposição dita-se verdadeira. Do mesmo modo, quando a característica atribuída ao sujeito não estiver segundo a realidade, a proposição dita-se falsa. Assim podemos concluir que a veracidade aplica-se unicamente ao conteúdo das proposições.
A validade e a invalidade estão inerentes aos argumentos e dizem respeito à sua forma, isto é, pela maneira como está organizado. Deste modo é desprezado o seu conteúdo.
Analogia – a conclusão tira-se através da comparação entre coisas distintas que apresentam características semelhantes.
Ex: Considerando as semelhanças anatómicas entre os homens e certos animais, inferimos que a reacção a certos medicamentos é idêntica em ambos. Daí serem usados animais como cobaias para experimentar medicamentos destinados aos seres humanos.
Nota: As conclusões a que chegamos a partir deste tipo de raciocínio podem ser mais ou menos prováveis, não nos oferecendo um grande grau de certeza.
Indutivo – neste tipo de raciocínio são tiradas conclusões universais a partir do conhecimento de casos particulares. A maioria das ciências experimentais recorre à indução.
Ex: A borracha é corpo e cai, a caneta é corpo e cai, o lápis é corpo e cai (…) Logo, todo o corpo cai.
Nota: As conclusões chegadas a partir da indução, tal como as chegadas a partir da analogia, não nos oferecem um grande grau de certeza, podendo ser mais ou menos prováveis.
Dedutivo – Aplica-se num caso particular o conhecimento que é geral. Deste modo, aceitando a verdade das premissas de que partimos, somos logicamente obrigados a aceitar a verdade da conclusão.
Ex: Todos os Homens são mortais. Sócrates é Homem. Logo, Sócrates é mortal.
Este silogismo é formado por três proposições, de tal maneira que, sendo dadas as duas primeiras (as premissas), se segue necessariamente a terceira (a conclusão). Deste modo, existe uma necessidade lógica entre as premissas e a conclusão, o que significa que, aceitando as premissas, somos obrigados a aceitar a conclusão.
É constituído por três e só três proposições, designadas por:
Existi ainda o termo Médio (M) que é o termo que estabelece o nexo lógico entre as premissas. Este termo nunca aparece na conclusão.
Ex:
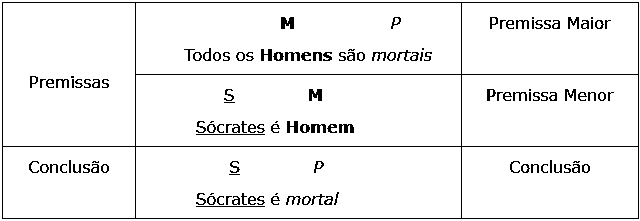

(Todos os exemplos abaixo enunciados correspondem a raciocínios inválidos)
Cada silogismo apenas pode ter três termo: o maior, o menor e o médio
Ex:
Este silogismo tem quatro termos. Na primeira premissa existe o termo “margarida” inerente à planta, enquanto no segundo existe o termo “Margarida” que corresponde a um nome próprio.
O termo médio nunca pode entrar na conclusão
Ex:
Como na conclusão o objectivo é obter a relação entre os termos extremos, o termo médio não pode aparecer.
O termo médio deve ser tomado pelo menos uma vez em toda a sua extensão
Ex:
Neste caso a conclusão tirada é inválida. Não temos como saber se entre os homens ricos existem ou não artistas.
Nenhum termo pode ter maior extensão na conclusão do que na premissa
Ex:
Na conclusão o termo “inteligentes” está tomado universalmente enquanto que na premissa não. Deste modo o raciocínio é inválido.
A conclusão segue sempre a parte mais fraca
Ex:
A parte mais fraca é negativa e particular. Se a conclusão segue sempre a parte mais fraca, então isso quer dizer que se alguma das premissas for particular, a conclusão tem que ser particular; que se alguma das premissas for negativa, a conclusão terá de ser negativa; e que se uma premissa for particular e a outra negativa, a conclusão terá que ser particular negativa.
De duas premissas negativas nada se pode concluir
Ex:
De duas premissas particulares, nada se pode concluir.
Ex:
De duas premissas afirmativas não se pode tirar uma conclusão negativa
Ex:
Neste caso a conclusão é ilegítima. Se as premissas são afirmativas a conclusão nunca pode ser negativa. Se for esse o caso, o raciocínio dita-se inválido.
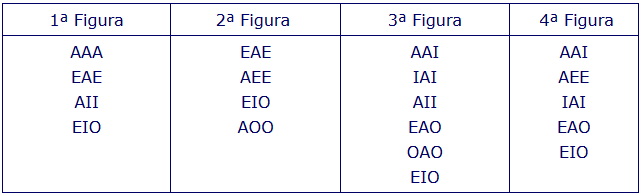
A forma do silogismo: o modo e a figura

O modo de um silogismo é indicado pelo tipo de proposições que o constituem (A, E, I, O). Existem 64 combinações possíveis, porém, nem todas são válidas; sendo algumas, apenas válidas em determinada figura.
Silogismo Hipotético ou Condicional
Um silogismo hipotético é aquele silogismo cuja premissa maior é uma proposição hipotética, sendo assim, constituída por:
Ex1:
Se chover, fico em casa
Está a chover,
Fico em casa
No exemplo mencionado, a premissa maior é uma proposição hipotética. Deste modo, é constituída por uma condição – “se chover” – e por um condicionado – “fico em casa”. Este exemplo esta no modo afirmativo ou Modus Ponens, já que a segunda premissa afirma a condição, para que o condicionado seja afirmado na conclusão.
Ex2:
Se chover, fico em casa
Não fico em casa,
Não está a chover
Neste exemplo, tal como no anterior, a premissa maior é uma proposição hipotética, sendo a sua condição “se chover” e seu condicionado “fico em casa”. Por outro lado, este exemplo está no modo negativo ou Modus Tollens, já que na segunda premissa o condicionado é negado, para que seja negada a condição na conclusão.
Silogismo Disjuntivo
Um silogismo disjuntivo é aquele cuja premissa maior é uma proposição disjuntiva. Tal como o silogismo hipotético, este tipo de silogismo também apresenta dois modos.
Ex1:
Ou te calas ou vais para a rua
Calas-te,
Não vais para a rua
O exemplo apresentado consiste num silogismo disjuntivo já que a premissa maior é uma proposição disjuntiva. O modo que apresenta é o Modus Ponendo-tollens, porque um dos membros é afirmado na segunda premissa, enquanto que o outro é negado na conclusão.
Ex2:
Ou chove ou faz sol
Não chove,
Faz sol
Tal como o anterior, este silogismo é disjuntivo, porém apresenta-se noutro modo, o Modus Tollendo-ponens, visto que um dos membros da premissa maior é negado na segunda premissa enquanto que o outro é afirmado na conclusão.
Falácias formais
Designa-se por falácia todo o raciocínio ou inferência que se apresenta inválido. Nas falácias distinguimos aquelas que são cometidas involuntariamente (paralogismos), das que são cometidas intencionalmente (sofismas).
Podem distinguir-se quatro principais tipos de falácias formais:
Todas estas falácias apresentadas estão relacionadas com a invalidade dos raciocínios mediantes as regras dos silogismos já referidas anteriormente.