
O teu país
Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod

Lorem ipsum dolor sit amet, consectetur adipiscing elit, sed do eiusmod
Todos os trabalhos publicados foram gentilmente enviados por estudantes – se também quiseres contribuir para apoiar o nosso portal faz como o(a) Nuno Alves e envia também os teus trabalhos, resumos e apontamentos para o nosso mail: geral@notapositiva.com.
Trabalho escolar sobre Sólidos Platónicos, realizado no âmbito da disciplina de Matemática (10º ano).
Os sólidos platónicos são sólidos convexos cujas arestas formam polígonos planos regulares congruentes. A sua designação deve-se a Platão, que os descobriu em cerca de 400 a.C.. A existência destes sólidos já era conhecida pelos pitagóricos, e os egípcios utilizaram alguns deles na arquitectura e noutros objectos que construíram.
Existem apenas cinco sólidos platónicos, que são os seguintes:
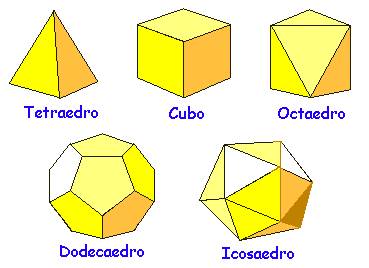
Estes sólidos foram adquirindo ao longo dos tempos diversos significados místicos. Por exemplo, Kepler sentia uma grande admiração e reverência por eles (Porquê apenas cinco?) e chegou mesmo a tentar explicar os movimentos planetários a partir deles. Além disso, interpretou, no Harmonices Mundi, as associações de Platão da seguinte forma:
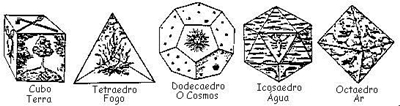
Uma demonstração de que são apenas cinco os sólidos platónicos pode ser obtida através do processo da sua construção, como Platão fez num seu texto incluído no diálogo Timeu.
Para a construção dos sólidos platónicos, por definição, apenas podemos utilizar polígonos regulares congruentes. Comecemos por considerar o triângulo equilátero, que é o polígono regular com menos lados. Quantos poliedros, cujas faces são apenas este polígono, conseguimos construir? Para responder a esta pergunta, centremos a nossa atenção nos vértices dos possíveis poliedros (basta considerar apenas um, pois os restantes são idênticos).
Com dois triângulos equiláteros, não se consegue constituir um vértice de um poliedro, pois um ângulo sólido tem que ser constituído pelo menos por três planos. Com três triângulos equiláteros é possível constituir um vértice de um poliedro, que é concretamente o tetraedro. Esta possibilidade prende-se com facto de a soma das amplitudes dos ângulos internos dos diversos triângulos adjantes, no vértice, ser inferior a 360º, exactamente 180º.
Se considerarmos quatro triângulos equiláteros, cuja soma das amplitudes dos ângulos internos adjantes no vértice é de 240º, obtemos o octaedro. Considerando cinco desses triângulos num vértice, essa soma é de 300º, ainda inferior a 360º, e obtemos o icosaedro. Passando para seis triângulos equiláteros, chegamos a uma impossibilidade. A soma das amplitudes dos ângulos internos adjantes no vértice é, neste caso, 360º, o que não permite "fechar" o vértice, isto é, formar um ângulo sólido, pois os triângulos ficam todos sobre o mesmo plano (formando uma pavimentação do plano em torno do suposto vértice). A consideração de um número maior de triângulos equiláteros em torno de um vértice, obviamente já não possibilita a construção de um poliedro.
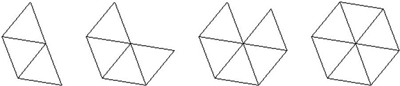
O pressuposto de construção que tem estado a ser utilizado é o de que a formação de um ângulo sólido no vértice de um poliedro só é possível se a soma das amplitudes dos ângulos internos dos polígonos adjacentes no vértce for inferior a 360º.
Considerando o quadrado, e o pressuposto atrás enunciado, chegamos à conclusão de que apenas conseguimos construir o cubo. Com pentágonos, apenas conseguimos construir o dodecaedro.
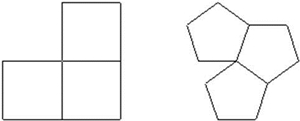
Com hexágonos não se consegue construir nenhum sólido platónico. Basta verificar que três hexágonos adjacente em torno de um ponto (supostamente um vértice) pavimentam o plano, pois a soma das amplitudes dos ângulos internos desses hexágonos é precisamente 360º, o que não permite formar um ângulo sólido. Um número maior de hexágonos, obviamente, que também não permite a construção de um sólido platónico. Analogamente, com polígonos com um número maior de lados isso também não é possível.
Enumeremos então os sólidos que acabámos de construir: tetraedro, octaedro, icosaedro, cubo e dodecaedro. São precisamente cinco, como se queria demonstrar.
Outra forma demonstrar a existência de apenas cinco sólidos platónicos é através da fórmula de Euler, considerando as restrições relativas aos vértices, arestas e faces inerentes aos sólidos platónicos.
Grandes filósofos e matemáticos dedicaram a vida ao estudo da geometria. Enquanto a escola pitagórica, por exemplo, tinha como lema "Tudo são números" a escola de Platão (a Academia) tinha escrito sobre a porta, "Não entre aqui ninguém que não seja geométra".
Platão foi o primeiro matemático a demonstrar que existem apenas cinco poliedros regulares: o cubo, o tetraedro o octaedro, o dodecaedro e o icosaedro. A eles se referiu no seu dialogo "Timeu" pelo que esses cinco poliedros regulares passaram a ser designados por sólidos platónicos.
O conhecimento destes sólidos parece ter sido desencadeado num encontro com Arquitas que, em viagem à Cecília, no sul de Itália, encontraria Platão. Para este, o Universo era formado por um corpo e uma alma, ou inteligência. Na matéria havia porções limitadas por triângulos ou quadrados, formando-se elementos que diferiam entre si pela natureza da forma das suas superfícies periféricas.
I. Se fossem quadradas, teríamos
o cubo - elemento terra.
II. Se fossem triângulos equiláteros, teríamos
o tetraedro - o elemento fogo.

o octaedro - o elemento ar.

o icosaedro - o elemento água.
III. Se fossem pentágonos, teríamos

o dodecaedro - simbolizava o Universo.
Embora chamados Platónicos, Proclus atribuiu a construção destes poliedros a Pitágoras, supondo-se que é também a ele que se deve o teorema: Há somente cinco poliedros regulares.
Hoje sabe-se que o teorema só é verdadeiro para os poliedros regulares convexos. Alguns séculos mais tarde, em 1597 Kepler, inspira-se nos poliedros regulares para estudar o movimento dos seis planetas até então conhecidos (Saturno, Júpiter, Marte, Terra, Vénus e Mercúrio) e publica a sua obra "The Cosmographic Mystery", onde utiliza um modelo do sistema solar composto por esferas concêntricas, separadas umas das outras por um cubo, um tetraedro, um dodecaedro, um octaedro e um icosaedro para explicar as distâncias relativas dos planetas ao sol.
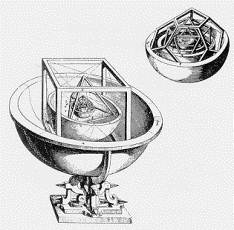
É também Kepler, que vai descobrir o primeiro poliedro regular côncavo, que é o dodecaedro estrelado, de faces regulares que resulta do prolongamento das faces do dodecaedro.

No séc. XVIII, Louis Poinsot descobriu três novos poliedros regulares não convexos.
Há nove poliedros regulares e Cauchy provou que não existem mais.
Poliedros (poli = muitos; hedros = faces) são sólidos delimitados por regiões planas (polígonos) que constituem as denominadas faces. Os segmentos de recta que limitam as faces designam-se por arestas e os pontos de encontro destas por vértices.
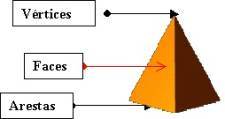
Um poliedro diz-se convexo quando os ângulos diedros formados por duas faces consecutivas forem menores que 180º.
Sólidos Platónicos são poliedros convexos cujas faces são polígonos regulares (polígonos com os lados e ângulos todos iguais) e que têm o mesmo número de faces que se encontram em cada vértice.

Se considerarmos um qualquer sólido platónico e "unirmos" os pontos centrais de faces adjacentes, obtemos um novo sólido platónico. Estes dizem-se duais um do outro.

Será que todos os poliedros regulares são convexos?
Kepler descobriu dois poliedros que são simultaneamente regulares e não convexos- o pequeno dodecaedro estrelado e o grande dodecaedro estrelado. Mais tarde, foi provado que existem apenas nove poliedros regulares, sendo cinco convexos (sólidos platónicos) e quatro não convexos (sólidos de Kepler-Poinsot).

Tetraedro:
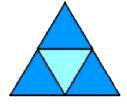
É um poliedro regular com 4 faces sendo estas triângulos equiláteros, 4 vértices e 6 arestas. O Tetraedro pode formar-se a partir de um molde com quatro triângulos.
Hexaedro ou Cubo:
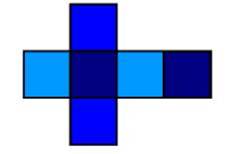
É um poliedro regular com 6 faces sendo estas quadrados, 8 vértices e 2 arestas. O cubo pode ser formado a partir de um molde com seis quadrados.
Octaedro:

É um poliedro regular com 8 faces sendo estas triângulos equiláteros, 6 vértices e 12 arestas. O octaedro pode ser formado a partir de um molde com oito triângulos equiláteros.
Icosaedro:

É um poliedro regular com 20 faces que são triângulos equiláteros, 12 vértices e 30 arestas. O icosaedro pode ser formado a partir de um molde de vinte triângulos equiláteros.
Dodecaedro:
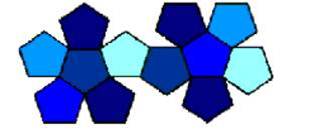
É um poliedro regular com 12 faces que são pentágonos, 20 vértices e 30 arestas. O dodecaedro pode formar-se a partir de um molde com vinte pentágonos.
Na geometria e algumas antigas teorias físicas, um solido platónico é um poliedro convexo com:
Os cinco sólidos platónicos, são conhecidos desde a antiguidade clássica, e a prova que são os únicos poliedros regulares pode ser encontrada nos Elementos de Euclides.
Tabela

Os alunos serão guiados a resolver alguns desafios mencionados ao longo do texto. Ao construir poliedros regulares, os alunos irão encontrar a fórmula de Euler, que quando aplicada a um dado poliedro regular convexo se conclui que esse poliedro terá de ser um dos cinco Sólidos Platónicos.
Discute-se o aparecimento de poliedros em estruturas moleculares da Biologia/Química. Finalmente introduz-se a noção de simetria e calcula-se o grupo das simetrias do tetraedro. Dado o uso de animações estas notas devem ser lidas usando a ligação via internet da página do encontro.
Os poliedros são estudados desde a Grécia Antiga na escola de Pitágoras, 600 aC, embora haja evidencia de que os Povos Neolíticos que viveram na Escócia tinham esculpidos alguns destes sólidos 1000 anos antes. Alguns destes modelos, ver figura 1, encontram-se no Museu Ashmolean em Oxford, Reino Unido.
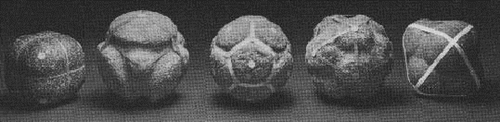
FIG 1: Modelos Neolíticos dos Sólidos Platónicos
Os poliedros ilustrados na figura 2 tiveram um papel crucial na Filosofia de Platão, que serão os nossos objectos de estudo.
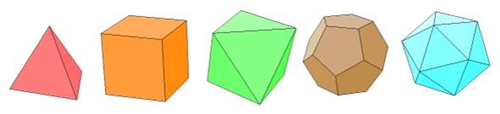
FIG 2: Tetraedro Cubo (Hexaedro) Octaedro Dodecaedro Icosaedro
Na sua admiração e entusiasmo (porquê só cinco?) pela Geometria, Euclides e a Grécia Antiga, chamou a estes os Sólidos Platónicos associando-os aos átomos do universo. Da mesma forma que hoje nós acreditamos que toda a matéria é feita de combinações de átomos, também na Grécia Antiga se acreditava que a matéria era feita com os sólidos Platónicos.
Também se acreditava que toda a matéria também tinha o lado místico. Assim, no diálogo Timaios, Platão associou o tetraedro ao elemento fogo, o cubo à terra, o icosaedro à água e finalmente o dodecaedro ao quinto elemento (o universo).

O cubo, tetraedro e o dodecaedro tinham sido considerados pelos pitagóricos, e os restantes por Theætetus – amigo de Platão -- que pensava que o universo estava envolvido por um dodecaedro gigante.
Os pitagóricos sabiam que existiam apenas cinco regular sólidos regulares convexos e que cada um podia ser rigorosamente circunscrito por uma esfera. Euclides descreve estes sólidos no seu livro Elementos, parte XIII, da proposição 13 à proposição 17, onde se encontra o argumento heurístico de que estes são os únicos sólidos regulares. O matemático Euler fez a demonstração deste resultado no séc. XVIII.
Kepler no início do séc. XVII, sugeriu associar os Sólidos Platónico aos planetas conhecidos nessa altura: Mercúrio, Vénus, Marte, Júpiter e Saturno.

Para resolver os seguintes desafios, será necessário fazer vários recortes dos seguintes polígonos:
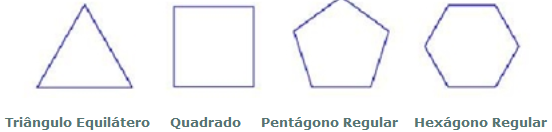
Desafio 1:
Desafio 2:
Desafio 3:
Desafio 4:
Obtém-se assim os cinco Sólidos Platónico e facilmente se conclui a seguinte tabela (como exercício, use a planificação destes sólidos para preencher esta tabela).
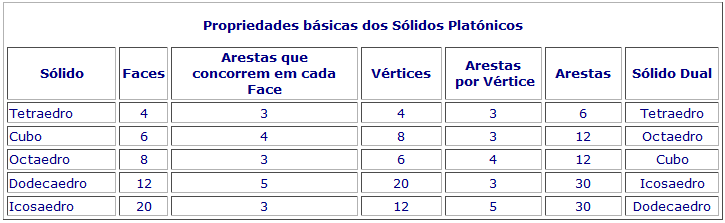
Formula de Euler (facto elementar da moderna topologia algébrica – ramo da Matemática): Seja P um poliedro convexo (não necessariamente regular), então temos:
onde F, A e V, denotam o número total de faces, arestas e vértices (respectivamente) do poliedro. Notamos que a primeira prova desta fórmula foi feita por Cauchy.
Desafio 5:
Verifique a validade da fórmula de Euler em cada um dos sólidos Platónicos!
Ligando os centros de todos as faces adjacentes de cada Sólido Platónico obtém-se assim um outro sólido (mais pequeno) que é novamente um Sólido Platónico. Designa-se por sólido dual a este sólido que se obteve a partir do inicial.
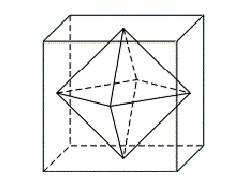
O dual do Cubo é o Octaedro
Como exemplo, temos que o Octaedro é o sólido dual do Cubo, como ilustra a figura 4.
Como o número de faces (vértices) do sólido dual é por construção igual ao número de vértices (faces) do sólido original, podemos então concluir a validade da última coluna da Tabela preenchida em cima.
Os Sólidos de Arquimedes ou poliedros semi-regulares são, grosso modo, poliedros convexos cujas faces são polígonos regulares de mais de um tipo. Todos os seus vértices são congruentes, isto é, existe o mesmo arranjo de polígonos em torno de cada vértice. Além disso, todo vértice pode ser transformado em outro vértice por uma simetria do poliedro. Existem apenas treze poliedros arquimedianos e são todos obtidos por operações sobre os Sólidos Platónicos. A título de exemplo, um deles designa-se por Icosaedro truncado e que é usada na moderna bola de futebol: 32 faces, 12 pentágonos, 20 hexágonos:
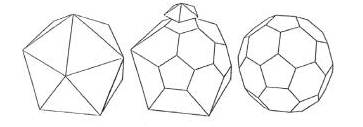
Construção da bola de futebol a partir do Icosaedro
Obtém-se assim a (moderna) bola de futebol:

Icosaedro truncado (ou bola de futebol ou ainda a molécula do futeboleno C60)
O Icosaedro truncado reencontrou novas e interessantes aplicações com a descoberta da molécula do futeboleno C60 (buckminsterfullereno ou buckyball) que foi comunicada num artigo da revista Nature, em 1985, por H. W. Kroto, J. R. Heath, S. C. O'Brien, R. F. Curl e R. E. Smalley. O primeiro e os dois últimos foram galardoados com o prémio Nobel da Química de 1996. Esta descoberta marca o início de uma nova área do conhecimento: a nanotecnologia. A molécula tem uma estrutura semelhante a uma bola de futebol. É constituída por 60 átomos de carbono, que formam 12 pentágonos e 20 hexágonos. Faz-se notar que se descobriu recentemente que muitos vírus, p.ex. o vírus da herpes, têm a forma de icosaedro!
Aliás, a ligação entre a estrutura geométrica dos átomos e alguns sólidos já tinha sido referida pelo próprio Platão, por exemplo: o sal mineral, i.e. cloreto de sódio NaSl, aparece na forma de cristais cúbicos; floreto de cálcio CaF2 na forma de octaedro e a pirite, i.e. Disulfito de Ferro FeS2 na forma de dodecaedros.
Os duais dos Sólidos de Arquimedes são designados por Sólidos de Catalan e a fórmula de Euler é válida para os poliedros convexos!
Uma vez que todos os poliedros convexos estão classificados é natural perguntar se haverá poliedros convexos que não sejam regulares?
Kepler, em 1619, descobriu dois poliedros que são simultaneamente regulares e não convexos: o pequeno dodecaedro estrelado e o grande dodecaedro estrelado.
Dois séculos mais tarde provar-se-ia que existem apenas nove poliedros regulares: os cinco sólidos platónicos e quatro poliedros regulares não convexos - os Poliedros de Kepler-Poinsot.
Um Poliedro de Kepler-Poinsot é um poliedro regular não convexo. Todas as suas faces são polígonos regulares iguais. E em todos os vértices encontram-se o mesmo número de faces (comparar com Sólidos Platónicos).
Existem quatro Poliedros de Kepler-Poinsot:
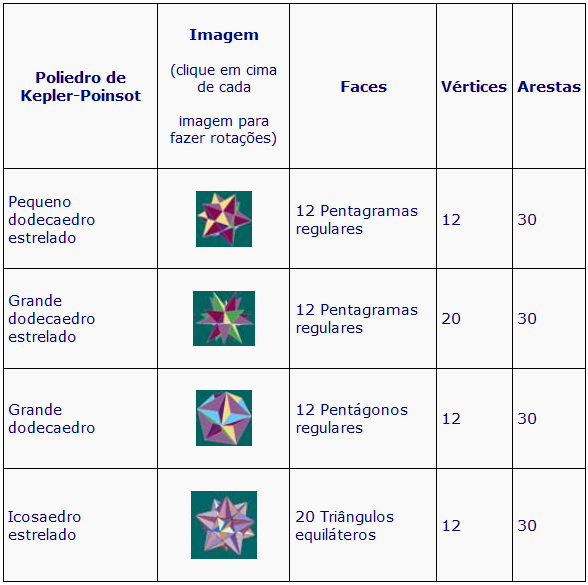
A formula de Euler não se verifica para dois deles --- Quais?
Assim temos apenas nove poliedros regulares, sendo cinco convexos (sólidos platónicos) e quatro não convexos (sólidos de Kepler-Poinsot).
Resumo:
(1) Existem exactamente 5 poliedros regulares convexos (os sólidos Platónicos)
(2) Existem exactamente 4 poliedros semi-regulares e convexos (sólidos de Arquimedes)
(3) Existem exactamente 13 poliedros regulares não convexos (sólidos de Kepler--Poinsot)