Home » Secundário » 10º Ano » Filosofia » A Lógica

A Lógica

Todos os trabalhos publicados foram gentilmente enviados por estudantes – se também quiseres contribuir para apoiar o nosso portal faz como o(a) Eliana Ferreira e envia também os teus trabalhos, resumos e apontamentos para o nosso mail: geral@notapositiva.com.

Resumo do trabalho

Resumo/Apontamentos sobre o tema "A Lógica", realizado no âmbito da disciplina de Filosofia (10º ano de escolaridade).

---

1.1. Validade e verdade

O que é a lógica?

Lógica: é o estudo das inferências ou argumentos válidos -> Raciocinar

Argumento: é um conjunto de proposições organizadas tendo em vista a defesa de uma determinada tese ou ponto de vista, de tal modo que a conclusão a que chagamos tenha por base uma outra ou outras proposições a que chamamos premissas.

Premissas: são as proposições usadas como ponto de partida ou justificação da conclusão.

Conclusão: é a proposição que deriva ou infere das premissas, sendo por estas justificada.

Inferência: é o processo que permite passar das premissas à conclusão.

Logo,

• A lógica estuda o processo de inferência para demonstrar a validade dos argumentos, isto é, para avaliar se a conclusão foi bem ou mal derivada das premissas ou se estas são uma boa razão para a sustentar.
• Um argumento cuja conclusão se segue das premissas é um argumento válido.
• O objectivo da lógica é compreender e demonstrar a validade dos argumentos e não a verdade das proposições que os constituem.

Argumento válido: todo aquele em que a conclusão é inferida correctamente, isto é, quando a conclusão decorre das premissas e é sustentada ou legitimada por elas.

Finalidades da lógica:

• Formular as regras a que os argumentos devem obedecer para serem válidos
• Distinguir as formas válidas das formas não válidas
• Desenvolver técnicas de avaliação dos argumentos

Princípios lógicos da razão:

• Princípio da identidade: todo o objecto é idêntico a si mesmo (A é A)
• Princípio da contradição ou da Não-contradição: não podemos afirmar ao mesmo tempo uma coisa e o seu oposto (não é verdade A e não A)
• Princípio do Terceiro Excluído: uma coisa é ou não é; não há uma terceira possibilidade ( A ou não A)

Se ao aprendermos a falar aprendemos os princípios da razão e as regras da lógica, qual o interesse e utilidade da aprendizagem da lógica?

• A lógica ensina a pensar, clara, concisa e correctamente
• A aprendizagem da lógica permite desenvolver capacidades de raciocínio e de argumentação e aumentar a capacidade de avaliação crítica dos argumentos
• Quem aprende lógica pensa de um modo mais preciso e comete menos erros

Frase declarativa e proposição

Frases declarativas: frases que dizem algo sobre a realidade tendo, por isso, valor de verdade.

Proposição: é o pensamento expresso numa frase declarativa (pode ser verdadeiro ou falso)

NOTA: As frases interrogativas, exclamativas e imperativas não expressam proposições, pois não têm valor de verdade.

A frase declarativa e a proposição estão profundamente ligadas (exprimir um pensamento implica o uso de uma linguagem), mas não são a mesma realidade:

• A mesma proposição pode ser expressa por frases declarativas diferentes (Ex: A utilidade da lógica é consensual./É óbvio que aprender lógica é útil.)
• Uma frase ambígua pode expressar proposições diferentes (Ex: A Joana viu o irmão com uns binóculos.)

Proposição e argumento

“Estudar lógica é útil para todas as pessoas porque aprender a argumentar com correcção facilita a comunicação e porque aprender lógica desenvolve a capacidade de argumentar.” (conectores)

Composto por:

3 frases declarativas/3 proposições:

Ø “Argumentar com correcção facilita a comunicação”

Ø “Estudar lógica desenvolve a capacidade de argumentar”

Ø “Estudar lógica é útil para todas as pessoas”

Premissas (razões ou pontos de partida)

Ø “Argumentar com correcção facilita a comunicação”

Ø “Estudar lógica desenvolve a capacidade de argumentar”

Conclusão

Ø “Logo, estudar lógica é útil para todas as pessoas”

O enunciado linguístico é um argumento porque é um conjunto de proposições relacionadas de modo a defender uma ideia (conclusão), apresentando razões para a justificar (premissas)

NOTA:

“Amanhã vai chover.”/”O clima está a sofrer alterações”

Ø Não são um argumento porque para que isso aconteça é preciso que as proposições estejam organizadas de modo a que uma seja a conclusão (o pensamento que se quer defender) e que as outras sejam tomadas como premissas (razões que a sustentam ou justificam)

Argumentos na forma padrão

Forma padrão ou forma canónica: modo estabelecido para apresentar o argumento, enunciando primeiro as premissas e a seguir a conclusão.

1. Enunciar a conclusão em primeiro lugar

“O ensino deve privilegiar o desenvolvimento de competências, uma vez que, hoje em dia, o conhecimento está disponível on-line e os cidadãos só precisam de saber procurá-lo, seleccioná-lo e fazer a sua apropriação pessoal”

Forma canónica ou padrão

Premissas:

Ø O conhecimento está disponível on-line.

Ø Os cidadãos só precisam de saber procurar, seleccionar e fazer a sua apropriação.

Conclusão:    

Ø   Logo, o ensino deve privilegiar o desenvolvimento de competências.

2. Enunciar a conclusão entre as premissas

“ A minha irmã adora cinema, por isso tenho a certeza de que vai gostar do Matrix, dado que não há apreciador de cinema que não goste do Matrix”.

Forma canónica ou padrão

Premissas:

Ø   Todos os apreciadores de cinema gostam do Matrix.

Ø   A minha irmã adora cinema.

Conclusão:

Ø   Portanto, a minha irmã vai gostar do Matrix

Logo,

Como devemos proceder perante um enunciado argumentativo?

Analisar o enunciado para identificar as premissas e a conclusão identificando indicadores de premissas e se conclusão.

Indicadores de premissas	Indicadores de conclusão
porque/visto que…/dado que…/por causa de…/como…/considerando que…/devido a…/uma vez que… (e outras expressões equivalentes)	logo…/portanto…/então…/por conseguinte…/segue-se que…/daí que…/consequentemente…/por isso…/infere-se que…. (e outras expressões equivalente)

Ø Para encontrar a conclusão: o que é que este argumento pretende demonstrar?

Ø Para encontrar as premissas: que razões ou justificações são apresentadas em favor da conclusão?

Explicitar eventuais premissas ocultas

Reescrever o argumento na forma canónica ou padrão

Validade e forma

Premissas:

Ø   Argumentar com correcção facilita a comunicação.

Ø   Estudar lógica desenvolve a capacidade de argumentar.

Conclusão:

Ø   Estudar lógica só tem utilidade para os programadores informáticos. (não decorre das premissas)

Este argumento não é válido:

• Ambas as premissas são verdadeiras e a conclusão também pode ser, mas esta não decorre das premissas;
• As premissas não sustentam nem legitimam a conclusão;

Validade: não depende da verdade ou da falsidade das proposições que constituem as premissas e a conclusão, mas do modo como estão relacionadas.

Validade lógica: é uma propriedade da estrutura dos argumentos, pois o tipo de relação estabelecido entre as premissas leva a uma determinada conclusão que é sempre verdade se as premissas forem verdadeiras.

Argumento válido: quando de premissas verdadeiras é impossível derivar uma conclusão falsa.

Forma lógica: é a estrutura de um argumento expressa no modo como estão relacionadas as diferentes proposições que o constituem, independentemente do conteúdo ou do que se diz.

Todos os A são B.

Todos os C são A.

Logo, todos os C são B.

Ex:

• Todos os portugueses (A) são europeus (B).
• Todos os lisboetas (C) são portugueses (A).
• Logo, todos os lisboetas (C) são europeus (B).

Se os argumentos não seguirem esta estrutura não podemos garantir que a verdade das premissas é preservada na conclusão.

RESUMO

Argumentos Um conjunto de proposições em que uma delas deriva da outra ou outras.	Proposições O pensamento expresso por uma frase declarativa. .
Forma válida Forma não válida	Verdadeiras             Falsas
Validade (propriedade dos argumentos) + Depende do tipo de conexão existente entre premissas e conclusão; + É independente do valor de verdade das proposições que constituem o argumento; + Um argumento pode ter premissas verdadeiras e conclusão verdadeira e não ser válido; + A validade garante a verdade da conclusão de um argumento que tenha que tenha premissas verdadeiras;	Verdade + Uma proposição é verdadeira quando expressa adequadamente as características da realidade a que se referem; . . . .

Forma lógica

LÓGICA ARISTOTÉLICA (substitui-se cada termo por uma letra maiúscula)

1. Todos os reactores(A) são rxz(B). Todos os mieglados(C) são rexatores. Logo, todos os mieglados são rxz.	Todos os A são B. Todos os B são C. Logo, todos os C são B.
2. Todos os alunos do Ensino Secundário (A) são submetidos a exames nacionais (B). Todos os alunos de 12º ano (C) são alunos do Ensino Secundário. Logo, todos os alunos de 12º ano são submetidos a exames nacionais.
3. Todos os alunos do 12º ano são alunos do Ensino Secundário. Alguns alunos de Matemática não são alunos do 12º ano. Logo, alguns alunos de Matemática não são alunos do Ensino Secundário.	Todos os A são B. Todos os B são C. Logo, alguns C não são B.

Conclusão:

Todos os argumentos têm um conteúdo diferente.

Os argumentos 1 e 2 têm a mesma forma./O argumento 3 tem forma diferente.

LÓGICA PROPOSICIONAL (SUBSTITUI-SE CADA PROPOSIÇÃO GLOBALMENTE POR UMA LETRA)

1. Todos os reactores são rxz. (P) Todos os mieglados são rexatores. (Q) Logo, todos os mieglados são rxz. (R)	P e Q, logo, R
2. Todos os alunos do Ensino Secundário são submetidos a exames nacionais. (P) Todos os alunos de 12º ano são alunos do Ensino Secundário. (Q) Logo, todos os alunos de 12º ano são submetidos a exames nacionais. (R)	P e Q, logo, R
3. Todos os alunos do 12º ano são alunos do Ensino Secundário. (P) Alguns alunos de Matemática não são alunos do 12º ano. (Q) Logo, alguns alunos de Matemática não são alunos do Ensino Secundário.	P ou Q, e Q, logo, não P

Conclusão:

Os três argumentos diferem quanto ao conteúdo.

Destacamos as expressões que definem a forma do argumento.

Repetem-se quando há identidade de forma e mudam quando o argumento tem forma diferente.

Os argumentos 1 e 2 têm a mesma forma. O argumento 3 difere dos outros dois na forma.

Logo,

Validade: refere-se à forma dos argumentos

Verdade: refere-se à matéria ou conteúdo, isto é, àquilo que é afirmado ou negado em cada proposição, traduzindo a adequação ou inadequação entre o pensamento expresso e a realidade a que se refere.

NOTA: A validade garante que a verdade das premissas vai ser preservada na conclusão.

Argumento sólido: argumento que é válido e tem premissas verdadeiras.

Inferências dedutivas e validade

Inferências dedutivas válidas: são aquelas em que a verdade das premissas é preservada na conclusão, em virtude da forma do argumento.

NOTA: A validade garante que num argumento dedutivo, seja impossível de premissas verdadeiras chegar a uma conclusão falsa.

Para termos a certeza de que as conclusões dos nossos argumentos dedutivos são verdadeiras, só temos de verificar se:

• Os argumentos são válidos
• As conclusões derivam de premissas verdadeiras

Uma conclusão é logicamente necessária: quando há apenas uma única possibilidade: a que decorre da forma do argumento. (Ex: Todos os seres vivos morrem e todos os homens são seres vivos, então, todos os homens morrem.) / (Ex: Todos os cisnes observados até agora eram negros. Logo, todos os cisnes são negros. > a conclusão não é logicamente necessária)

Argumentos dedutivos: aqueles cuja conclusão é logicamente necessária

Argumentos não dedutivos: aqueles cujas premissas apoiam, mas não garantem, a verdade da conclusão.

1.2. Formas de inferência válida

O conceito e o termo

Conceito: representação mental abstracta e universal que designa, na mentem um conjunto ou uma classe de objectos ou de seres. (o significado ou a ideia)

Termo: o conceito expressa-se verbalmente pelo termo.

Conceptualização: processo de formação de conceitos.

• Analisar os dados da experiência
• Identificar características comuns aos elementos de um grupo
• Abstrair (isto é, separar e ignorar diferenças individuais ou de subgrupos)
• Sintetizar numa representação mental as características que definem a compreensão do conceito
• Generalizar, aplicar a todos os indivíduos de um conjunto

Compreensão ou intenção de um conceito: características que o definem como tal.

Extensão ou denotação: conjunto de seres a que o conceito se aplica.

O juízo e a proposição

Ex: O cão é meigo.

• Sujeito lógico: aquilo de que se diz alguma coisa
• Predicado lógico: aquilo que é afirmado ou negado como atributo ou qualidade do sujeito

Ø A cópula estabelece a relação entre os dois termos (verbo ser)

Juízo: operação mental que estabelece a relação entre um sujeito e um predicado, afirmando ou negando que um certo predicado convém ao sujeito.

Frase declarativa: expressão ou enunciado linguístico do juízo.

Proposição: pensamento expresso na frase declarativa.

Forma: modo como estão relacionados os termos numa proposição.

Matéria: conteúdo, isto é, aquilo que é afirmado ou negado acerca do sujeito.

Se dissermos:

• S é P ou S não é P: estamos a expressar a qualidade da forma, que pode ser negativa ou afirmativa, conforme a cópula afirma ou nega (natureza da cópula)
• Todo o S é P ou Algum S é P: estamos a expressar a quantidade da proposição, estabelecida a partir da extensão em que se toma o sujeito.

Podemos classificar as proposições quanto à:

Qualidade, ou natureza da cópula:

Ø Afirmativas (é): afirmam que o predicado convém ao sujeito

Ø Negativas (não é): negam que o predicado convém ao sujeito

Quantidade, ou extensão do sujeito:

Ø Universais (todos): o predicado aplica-se à totalidade dos elementos que constituem a extensão do sujeito

Ø Particulares (alguns): o predicada aplica-se a parte dos elementos que constituem a extensão do conceito

A combinação entre a quantidade e qualidade das proposições leva-nos a 4 tipos de proposições

Tipo	Qualidade	Quantidade	Exemplo
A	Afirmativa	Universal	Todas as invenções são úteis
E	Negativa	Universal	Nenhuma invenção é útil. (forma padrão de: Todas as invenções não são úteis.)
I	Afirmativa	Particular	Algumas invenções são úteis.
O	Negativa	Particular	Algumas invenções não são úteis.

A quantidade de uma proposição é definida por palavras a que chamamos quantificadores: indicam-nos se o sujeito se refere a todos os elementos do conceito ou apenas a uma parte deles (quantificadores universais: todo/nenhum/qualquer || quantificadores particulares: algum/poucos/certos/nem todos);

Inferências imediatas

“Quadrado lógico de oposição” entre proposições

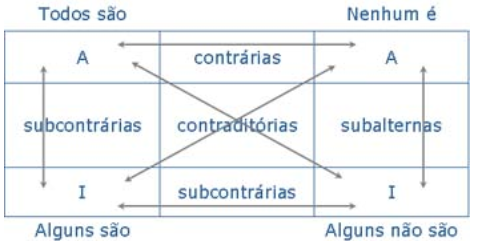
Oposição de proposições	Exemplos	Regras
Contraditórias: as proposições diferem na quantidade e na qualidade	A. Todos os advogados são juristas. O. Alguns advogados são juristas. E. Nenhum advogado é jurista. I. Alguns advogados são juristas.	Não podem ser verdadeiras nem falsas ao mesmo tempo. Se A é verdadeira, O é falsa Se E é verdadeira, I é falsa
Contrárias: as proposições são universais, mas diferem na qualidade	A.       Todos os advogados são juristas. E.   Nenhum advogado é jurista.	Não podem ser verdadeiras ao mesmo tempo , mas podem ser falsas ao mesmo tempo
Subcontrárias: ambas as proposições são particulares, diferem na qualidade	I.    Alguns advogados são juristas. O.   Alguns advogados são juristas.	Podem ser ambas verdadeiras ao mesmo tempo. Não podem ser as duas falsas ao mesmo tempo.
Subalternas: ambas as proposições são afirmativas ou negativas, diferem na quantidade	B.      Todos os advogados são juristas. O.   Alguns advogados são juristas. E.   Nenhum advogado é jurista. I.    Alguns advogados são juristas.	Se a universal é verdade, a particular é verdadeira Se a particular é falsa, a universal é falsa.

Distribuição dos termos

Está distribuído: é tomado em toda a sua extensão ( refere-se a todos os elementos a que o conceito se aplica/afirma algo de todos e de cada um dos elementos que designa)

Não está distribuído: é tomado apenas em parte da sua extensão (refere-se a alguns elementos que pertencem à extensão do sujeito)

Ex: Todos os ruminantes são herbívoros.

Ø Ruminantes: está distribuído

Ø Herbívoros: não está distribuído (refere-se só aos ruminantes)

A (Todo o S é algum P) Ø Sujeito distribuído Ø Predicado não distribuído

E (Nenhum S é (nenhum) P) Ø Sujeito distribuído Ø Predicado distribuído

I (Algum S é (algum) P) Ø Sujeito não distribuído Ø Predicado não distribuído

O (Algum S não é (nenhum) P) Ø Sujeito não distribuído Ø Predicado distribuído

O silogismo categórico

Uma proposição é categórica quando afirma ou nega algo de forma absoluta e incondicional.

Proposição:

Ø 2 termos

Ø Cópula

Silogismo:

Ø 3 termos

Ø 3 proposições

Ø Cada um dos termos aparece 2 vezes

Silogismo categórico

Três proposições:

Ø Premissa maior:

¨ Contém o termo maior, isto é, de maior extensão

Ø Premissa menor:

¨      Contém o termo menor

Ø Conclusão:

¨ Decorre da relação estabelecida entre as premissas

¨ Contém o termo maior (P) e o menor (S)

¨ Não contém o termo médio

Três termos:

Ø Maior (P):

¨ O termo de maior extensão

¨ Predicado da conclusão

Ø Menor (S):

¨ O termo de menor extensão

¨ Sujeito da conclusão

Ø Médio (M):

¨ Aparece nas duas premissas e não está na conclusão

¨ Estabelece a ligação entre os outros termos

Nexo lógico:

Ø Estabelecido pelo termo médio

Ø A articulação entre as premissas é que permite derivar delas a conclusão

Regras dos termos

1. Um silogismo tem de ter três e só três termos

Ex:

O fim de uma coisa é sua perfeição.

O fim da vida é a morte.

Logo, a morte é a perfeição da vida. (não é válido: “fim” é um termo ambíguo/relação entre 4 termos e não 3)

2. O termo médio não pode aparecer na conclusão

Ex infracção:

Sócrates é filósofo.

Sócrates é pequeno.

Logo, Sócrates é pequeno filósofo.

3. O termo médio tem de ser tomado pelo menos uma vez em toda a sua extensão (universalmente), ou seja, deve estar distribuído pelo menos uma vez.

Ex infracção:

Todos os leões são mamíferos.

Todos os gatos são mamíferos.

Logo, todos os gatos são leões.

4. Nenhum termo pode ter maior extensão na conclusão do que nas premissas, ou seja, se um termo está distribuído na conclusão tem de estar distribuído na premissa onde ocorre.

Ex infracção:

Todos os carnívoros são seres vivos.

Alguns mamíferos não são carnívoros.

Logo, nenhum mamífero é um ser vivo.

Regras das proposições

1. De duas premissas (proposições) negativas nada se pode concluir.
2. De duas premissas afirmativas não se pode derivar uma conclusão negativa.
3. A conclusão segue sempre a parte mais fraca, isto é, se uma das premissas for particular, a conclusão terá de ser particular, e se for negativa, a conclusão será negativa.
4. De duas premissas particulares nada se pode concluir.

Figuras do silogismo categórico

Figuras: resultam da posição do termo médio nas premissas

Modos: resultam da qualidade (afirmativa/negativa) e da quantidade (universal/particular) das proposições.

Sujeito da premissa maior e predicado da premissa menor

1ª figura

M > P

S > M

S > P

Predicado em ambas as premissas

2ª figura

P > M

S > M

S > P

Sujeito em ambas as premissas

3ª figura

M > P

M > S

S > P

Predicado de premissa maior e sujeito da premissa menor

4ª figura

P > M

M > S

S > P

Modos do silogismo categórico (não preciso saber)

Falácias formais do silogismo categórico

Falácias formais: argumentos que não cumprem as regras lógicas de inferência.

Falácias:

¨ Formais: os argumentos que não cumprem as regras lógicas de inferência

¨ Informais: os argumentos cujos erros são derivados da matéria ou do conteúdo das premissas.

Principais falácias formais do silogismo:

Quatro termos

Termo médio não distribuído

Ilícita maior (quando o termo médio apresenta maior extensão na conclusão do que nas premissas)

Ilícita menor (quando o termo menor apresenta maior extensão na conclusão

321 Visualizações 21/09/2019

---